Le programme de mathématiques
Au lycée, LA matière souvent considérée comme la plus scientifique est la matière dédiée aux mathématiques. Elle est probablement une des matières les plus fantasmées et craintes au lycée. Sur cette page, nous n'allons pas expliquer chaque concepts un par un précisément comme en cours, mais plutôt décortiquer le programme et expliquer comment et pourquoi il est fait. Bien évidemment, nous allons utiliser le programme fourni par l'éducation nationale pour l'année 2024-2025.
Bien évidemment, tout cela ne reflète que notre analyse personelle. Si vous avez des professeurs différents, certaines notions peuvent être vues de manière différente. Cependant, une grande partie des professeurs font de la même manière : commencer par le début et finir par la fin. Donc, les divergences ne devraient pas être si élevées que ça.

Quelques détails
Comment lire cette page ?
Cette page n'est pas un ensemble de leçon pour les élèves, comme il ne s'agit pas d'un guide pour réaliser ses cours en tant que professeur. Cette page n'est pas non plus là pour directement critiquer le programme. Au contraire, cette page est sensée servir de présentation du programme à tous individus extérieurs / prochainement intérieurs au lycée, agrémenter de quelques précisions et commentaires. Par exemple, si vous avez pour projet de choisir cette enseignement de spécialité pour la terminal (ou pour la première), voici sur quoi vous allez travailler. Mais aussi, si vous voulez devenir professeur de mathématiques, voici les sujets sur lesquelles vous allez devoir travailler avec vos élèves. Si vous avez déjà cette spécialité, et que vous voulez donner un avis, n'hésitez pas à nous contacter à astersystemelearnoff@gmail.com. Si vous cherchez des sujets de BAC, vous pouvez en trouver sur ce site web. L'avantage de l'ère du tout numérique est que beaucoup d'infos sont facilement obstensibles sur Internet, rendant une grande partie des nouveaux inscrits particulièrement doué. C'est pour cela que, si vous êtes doués, n'hésitez pas à aider vos camarades. Si vous êtes un professeur, avec plusieurs élèves doués, n'hésitez pas à les missionner pour aider les autres, il n'y aura que des avantages !

Premier trimestre
Dans cette partie, je vous présenterai tout ce que vous avez probablement fait lors du premier trimestre de l'année de mathématiques.
L'analyse de suites et de fonctions
Les suites mathématiques sont abordées en première. Les suites sont des fonctions définies au maximum sur l'ensemble des entiers naturels. Nous avons déjà parlé des fonctions sur notre site web, sur la page dédiée à l'algèbre. En bref, il s'agit d'une transformation applicable à un objet mathématique (vers un autre), très souvent des nombres réels ou naturels en terminale. Avant tout de chose, les acquies de premières sont rappelés (suites arithmétiques, suites géométriques, suites récurrentes...). En réalité, l'utilisation de suite est un moyen d'amorcer vers des concepts de fonctions de manière plus simple. Cependant, un exemple échappe à cette règle. En effet, l'usage de suite permet d'introduire une nouvelle méthode de raisonnement : le raisonnement par récurrence. L'idée de ce raisonnement est de raisonner en justifiant qu'une hypothèse sur un élément d'une suite est vraie, et que, dans le cas des éléments qui suivent, l'hypothèse est vraie SI ET SEULEMENT SI l'hypothèse de l'élement d'avant est vraie. Dans ce cas, comme la première est vraie, la deuxième le sera, et donc la troisième... Cette méthode est introduite pour élargir les méthodes démonstratives des élèves, dans le cas des suites.
Parmi les concepts étudiés pour les suites, puis pour les fonctions, se trouve la notion de limite. En mathématique, une limite de fonction représente une valeur théorique, atteignable lorsque l'on fait tendre une fonction vers + l'infini, - l'infini, ou vers une borne de l'ensemble de définition. Ici, "tendre" signifie se rapprocher très prêt d'une valeur. De plus, nous pouvons définir des fonctions convergentes en une certaine valeur, si elles ont une limite existante tendant vers cette certaine valeur. À l'inverse, une fonction n'admettant pas de limite est dite divergente (comme les fonctions sinus ou cosinus). Si une fonction converge en + l'infini ou - l'infini VERS une valeur n'étant pas l'infini, il est possible de créer une équation de droite de cette valeur, nommée une asymptote horizontale (auquelle la courbe tracée par la fonction va petit à petit s'approcher) de la courbe de la fonction. De manière très similaire, une fonction convergeante en une valeur finie VERS + ou - l'infini rend possible la création d'une équation de droite à cette valeur, nommée asymptote verticale de la courbe de la fonction. Cependant, il peut arriver qu'une limite en une certaine valeur PUISSE avoir deux limites : une pour des valeurs de x inférieures et une pour des valeurs de x supérieures. Dans ce cas, on parle de limite à gauche (inférieure) et à droite (supérieure).
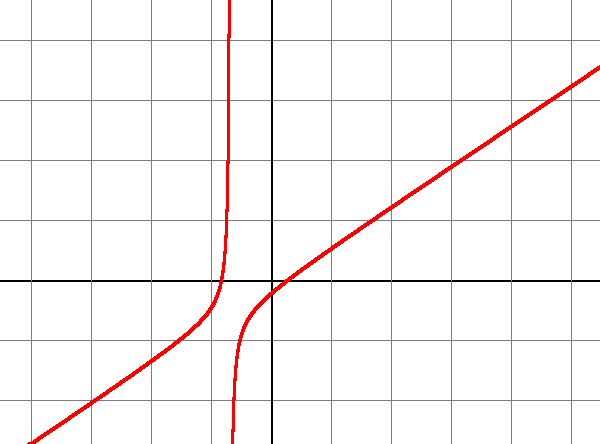
Dans cette exemple, on peut conjecturer graphiquement que la fonction décrite par cette courbe tend vers + l'infini en + l'infini et vers - l'infini en - l'infini. De plus, si elle tend vers -0.7, la fonction converge vers + l'infini à gauche et - l'infini à droite. Donc, cette courbe admet une asymptote verticale, d'équation de droite "y = -0.7".
La démonstration mathématique de l'existence d'une limite est assez simple. Dans le cas des limites en x vers + ou - l'infini, cette limite existe si, pour un quelconque nombre réel M, il existe une valeur de la fonction supérieure / inférieure à M lorsque l'on tend vers x. Une autre façon de dire est que si plus on se rapproche d'une valeur, plus l'image de la fonction est grande / petite, alors elle tend vers + l'infini / - l'infini en cette valeur. Par exemple, pour une fonction f définie sur R tel que f(x) = x * x, on sait que f(x) sera supérieure à M dés f(sqrt(M)) lorsque l'on fait tendre x (et donc M) vers + l'infini, quelque soit M : elle tend donc en + l'infini, vers + l'infini. À l'inverse, on sait que f(x) sera supérieure à M dés f(sqrt(|M|)) lorsque l'on x tend vers - l'infini (et donc M vers + l'infini) : elle tend donc en + l'infini vers - l'infini. Dans le cas d'une fonction g définie sur R* tel que g(x) = 1/x, on sait que g(x) sera supérieure à M dés f(1/M) lorsque l'on tend x vers 0 (et donc M vers + l'infini) : elle admet donc une limite en 0, vers + l'infini. Si la limite vaut une valeur précise M en x, cette limite existe si, pour une valeur E toujours plus proche de x, il existe toujours un nombre réel P plus grand que la différence entre f(E) et M. Une autre façon de dire est que si plus on se rapproche d'une valeur x, plus l'image de la fonction est proche de M, alors elle tend vers M en x. Par exemple, pour une fonction f définie sur R* tel que f(x) = 3 + 1/x, on sait que la différence entre f(E) et 3 sera de 1/E, tendant vers 0 pour E tendant vers + l'infini : f admet donc une limite en + l'infini, vers 3. Heureusement, il existe des formes bien connues pour convertir une fonction complexe en sa valeur directe. Il est aussi possible de faire des opérations avec des limites, pour obtenir des limites de fonctions plus complexes :
| Valeur | Limite en + l'infini | Limite en - l'infini |
| a constante | a | a |
| a * x avec a > 0 | + l'infini | - l'infini |
| a * x avec a < 0 | - l'infini | + l'infini |
| a / x avec a différent de 0 | 0 | 0 |
Pour en finir avec les fonctions, un autre concept étudié est le concept de dérivation. Théoriquement, la dérivation est étudiée en première. En terminale, le concept est affiné pour plus de détails. Les dérivées secondes (dérivées de dérivées) et les concepts de convexité et concavité sont abordés. Pour étudier cela, le concept de corde est introduit. Ici, une corde représente un segment (obstensible via une équation de droite) entre deux points de la courbe tracée par la fonction. Localement (entre les deux points du segment), la fonction est concave si l'entiéreté des valeurs de la fonction sont supérieures à celles du segment (si la courbe est au dessus du segment). À l'inverse, elle est convexe si l'entiéreté des valeurs de la fonction sont inférieures à celles du segment (si la courbe est en-dessous du segment). Cependant, le signe de la dérivée seconde permet de savoir si une fonction est concave ou convexe en un point précis. Si la dérivée seconde est négative, la fonction est concave, et si elle est positive, la fonction est convexe. En réalité, les dérivées secondes représentent les accélérations (ou freinages) des variations de la fonction, expliquant pourquoi elles sont nécessaires ici. En revanche, si le signe de la dérivée seconde s'inverse, la fonction passe de concave à convexe (ou de convexe à concave). Cet endroit est nommé un point d'inflexion.
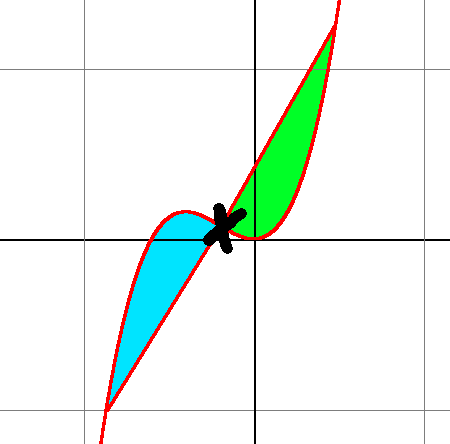
Nous avons la fonction définie sur l'ensemble des réels par : Sur cette fonction, toute la partie bleue est concave, et la partie verte est convexe. Le point d'inflexion se trouve là où est la croix. Cette fonction est dérivable deux fois sur R. Nous pouvons calculer la dérivée première et seconde de cette fonction. Cette fonction est inférieure à 0 de - l'infini à -1/6, elle est donc concave sur cette intervalle. De -1/6 à + l'infini, elle est donc convexe. Comme elle s'annule pour x = -1/6, on sait donc qu'il s'agit du point d'inflexion de f.
La géométrie
Tout cela ne serait pas drôle sans géométrie. Nous commençons avec toutes les bases définies en première : vecteurs, relation de Chasles (et, plus implicitement, toute l'algèbre "basique" des vecteurs), combinaisons linéaires.... Ici, l'idée est d'approfondir ces concepts.
Le premier concept abordé est les plans et droites de l'espace 3D. Ici, un plan représente une surface 2D dans un espace 3D, et une droite représente une ligne dans ce même espace. Pour les caractériser, le concept de vecteur directeur de plans et de droites est introduit. On peut définir un plan avec deux droites sécantes (et leurs vecteurs directeurs). Le terme "coplanaire" est aussi introduit, représentant des vecteurs (ou des points / droites) sur le même plan. Ce terme rejoint le concept de plans et droites sécantes entre eux / elles, ainsi que de droites et plans parallèles, et finalement de vecteurs colinéaires. Grâce à ces termes, on peut aussi parler de positions relatives entres objets géométriques, pour savoir si plusieurs objets partagent ces caractéristiques. De plus, la présence de plan permet de définir des sous-espaces 2D sur ce plan, permettant de faire du calcul via ce plan. Par exemple, pour savoir si un vecteur est sur un plan, il suffit de savoir si il existe une combinaison linéaire via un repère de ce plan.
Pour utiliser tous ces termes de manière calculatoire, une formule très utile est aussi introduite : la représentation paramétrique d'une droite. La représentation paramétrique d'une droite représente un système d'équation permettant de savoir quels points appartiennent à la droite. Voici un la représentation pure d'une représentation paramétrique de droite :
Ici, u(a, b, c) représente un vecteur directeur de la droite et p(e, f, g) représente un point quelconque de la droite. En réalité, il existe une infinité de représentations possibles. Grâce à cette représentation, il est possible de lier tous les calculs présentés au-dessus, pour étudier proprement la géométrie en 3D.
Les probabilités
Les probabilités sont considérées comme un des chapitres les plus simples du programme. Bien évidemment, ils s'agit encore d'approfondissement de notions déjà connues : univers, épreuves, évènements... En terminale, l'accent est mit sur la loi binomiale. Dans ce domaine, la loi binomiale est un moyen de représenter une suite d'évènements spéciaux, nommés des épreuves de Bernoulli. Une épreuve de Bernoulli est une épreuve amenant à deux issues, nommées succès et échec. En toute logique, le succès a une certaine probabilité d'arrivée, et l'échec la probabilité inverse. Une suite d'une même épreuve de Bernoulli indépendante est appelée un schéma de Bernoulli, représentable sous forme d'arbre pondéré. La correspondance d'un schéma de Bernoulli et de sa probabilité de succés est nommé une loi binomiale.
