La logique

La logique pure

Qu'est ce que la logique ?

En termes généraux, la logique représente un ensemble de règles permettant de justifier correctement un propos. Par exemple, l'affirmation "je suis une licorne" demande une justification logique pour être acceptée (justification impossible à produire ici, car les licornes n'existent pas). Cependant, l'affirmation "je suis un homme", qui demande une justification logique pour être acceptée, peut être justifiée par l'apport d'une photo de ma carte d'identité (et une explication de pourquoi elle prouve que je suis un homme pour plus de rigueur). Elle rend aussi possible la jonction de plusieurs affirmations pour en former une nouvelle, comme les deux affirmations "la carte d'identité permet de prouver mon genre" et "ma carte d'identité indique que je suis un homme", qui permettent de prouver "je suis un homme". Cette definition là est applicable pour tout ce qui se passe dans nos vies.

La logique mathématique

Appliquer la logique aux mathématiques

En mathématiques, le sens est très similaire, mais plus précis pour mieux coller à la discipline. En mathématiques, la logique représente un ensemble de règles permettant de justifier correctement un propos dans le langage des mathématiques. Elle fait intervenir la possibilité d'utilisation des outils mathématiques, comme les nombres ou les inconnus (et tout ce qui en découle : théorèmes, calculs...). Comme tous concepts de ce genre, elle utilise son propre langage, décrit plus loin.

Les axiomes

Comme pour la logique simple, la logique en mathématique permet de former une affirmation à partir d'autres affirmations plus primaires. En mathématique, les affirmations les plus primaires de chaque branches sont nommées des axiomes. Les axiomes sont des propositions théoriquement indémontrées (mais qui, en pratique, sont tout à fait """"logiques""""", en accord avec les autres sciences et ne nécessitent pas de démonstration) qui servent de bases à toutes les mathématiques. En général, chaque branche utilise plusieurs axiomes différents, comme la géométrie qui peut utiliser les 26 axiomes de Hilbert. Grâce à ces axiomes, on peut réaliser des propositions un peu plus complexes, nommées des démonstrations. Les démonstrations peuvent utiliser plusieurs axiomes, ou d'autres démonstrations (pouvant utiliser eux même des axiomes ou d'autres démonstrations...). Ce phénomène de lien axiomes-théorèmes est nommée la déduction logique. D'ailleurs, une affirmation démontrée comme vraie est nommée un théorème. Une immense quantité de théorèmes existent, comme le théorème de Pythagore (assez simple à démontrer).

L'alphabet de la logique

La théorie des langages

Avant de définir les symbôles mathématiques, nous allons déjà revoir quelques bases de la théorie des langages (oui, ça existe) en mathématiques. Selon cette théorie, un langage représente un ensemble de mots. Cependant, selon le contexte, un "mot" peut avoir plusieurs définitions (dans le cas du français, un mot est, bien évidemment, une suite de lettres). En mathématiques, un "mot" représente un ensemble d'éléments mathématiques, nommés des... lettres. Les différents symbôles sont tous présents dans un ensemble nommé un alphabet. D'ailleurs, il existe une opération pour les lettres : la concaténation. Ici, la concaténation représente la création d'un mot en ajoutant un mot (ou une lettre) à la suite d'un autre. Voici un exemple de cette opération.

Salut + ation = Salutation

L'exemple le plus utilisé ici est la langue française. Dans ce cas, l'alphabet utilisé est l'alphabet latin, avec 26 letters différentes(sans compter les versions modifiées : ç, à...). En mathématique, cela est très similaire. En effet, l'alphabet représente un assemblage de chiffre, d'opérateurs et de variables. Cependant, elle implique beaucoup plus de domaines d'études qu'implique la théorie des langages.

La grammaire formelle

Si nous parlons de cette théorie ici, c'est essentiellement pour ce concept. La grammaire formelle représente l'ensemble des règles permettant de donner sens à un langage. Pour les langages dans l'algèbre, cela est nommé la grammaire algébrique. Bien que ce concept puisse faire peur, il s'agit en réalité de la base de tous les langages existant. Un exemple (infiniment évident) de règle est : "les mots sont séparés par des espaces".

La définition mathématique de ses règles est un peu plus complexe que ça. Premièrement, nous allons définir un ensemble symbôles, que nous appellerons symbôles terminaux(ici, il faut interpréter "terminaux" comme "derniers"). Deuxièmement, nous allons définir un autre ensemble de symbôles (différents de la 1ère), que nous appellerons symbôles non-terminaux (ici, il faut interpréter "non-terminaux" comme "pas les derniers"). Troisièmement, nous allons choisir un des symbôles non-terminaux, qui sera la base de notre mot (ou phrase) : nous allons l'appeller l'axiome. Finalement, nous allons devoir définir les règles des symbôles non-terminaux. En effet, l'idée ici est de partir d'éléments non-terminaux, et de les remplacer par autre chose(comme un mot). C'est pour cela qu'on les appelle non-terminaux ("pas les derniers", ils vont être remplacés par autre chose). Les règles permettent de savoir par quoi les remplacer. On peut en définir plusieurs, que l'utilisateur peut utiliser comme il le souhaite. L'idée est de les remplacer par une suite de symbôles terminaux ("derniers", qui ne seront plus remplacés), ou de symbôles non-terminaux (qui, plus tard, seront remplacer par une suite de symbôles terminaux), voir par rien du tout si l'on veut. Il s'agit donc d'une construction récursive.

Pour noter ce genre de règle, nous pouvons utiliser une notation précise : la forme de Backus-Naur. Dans cette notation, les symbôles non-terminaux sont entre chevrons et les symbôles terminaux ne sont pas entre chevrons. De plus, l'espace texte est coupé en 2 (par des |) : la partie gauche représente les symbôles terminaux, et la partie droite représente les règles de ses symbôles (un par ligne). Il est à noter que cette façon de faire est généralement utilisé pour des langages de programmations informatiques, mais peuvent aussi être utilisé pour des langages mathématiques.

Selon les règles précises de sa grammaire, un langage peut être interpréter mathématiquement de manière différente. Pour classer les langages, nous pouvons utiliser une hiérarchie précise : la hiérarchie de Chomsky. Un langage est de type 3 si chaque règles des non-terminaux les transforment en une quelconque suite de symbôles terminaux ou non-terminaux SAUF eux-mêmes. Ces langages sont dit rationnels. Un langage est de type 2 si chaque règles des non-terminaux les transforment en une quelconque suite de symbôles terminaux ou non-terminaux. Dans ce cas, ces langages sont dis algébriques (ou non-contextuelles). Un langage est de type 1 si il est de type 2 ou 3 et certaines règles des non-terminaux demandent à ce que les non terminaux se trouvent dans un certain contexte. Par exemple, un remplacement ne peut avoir lieu que si un non-terminaux est entouré de certains symbôles spécifiques. Bien évidemment, l'axiome ne doit pas être contextuel, car sinon il ne peut pas exister. Ces langages sont dit contextuels, et englobent les langages naturels (le français, l'anglais...). Finalement, un langage est de type 0 si il est défini par une grammaire quelconque. Plus un langage est de type élevé, plus il est facile à étudier.

Une façon de voir la logique

Qu'est ce qu'est une proposition ?

En logique mathématique, une proposition représente une information quelconque. Cependant, cette information ne peut avoir qu'une valeur : elle peut être vraie ou fausse. Par exemple, "je suis beau" est une proposition, puis ce qu'elle représente une information est soit vraie, soit fausse. Une logique n'utilisant que ce genre de propositions (vraies ou fausses) est dite bivalente.

Certaines propositions sont obligatoirement vraie, quoi qu'il arrive. Les propositions vraies dans tous les contextes possibles sont nommées des tautologies. Un exemple de tautologie est : "SI NON P IMPLIQUE P, ALORS P". Cette tautologie est assez étrange : elle exprime que si la véracité de "NON P" implique "P", alors "P" est toujours vraie. En réalité, c'est parfaitement logique : si une proposition ne PEUT être fausse que quand elle est vraie, alors elle est toujours vraie (puisqu'elle ne peut pas être fausse autrement, et qu'elle ne peut pas être les deux en même temps). De manière vulgarisée, une propriété qui ne peut pas être fausse est vraie (à l'inverse, une propriété qui ne peut pas être vraie est fausse). Cette forme de raisonnement est nommée le raisonnement par l'absurde.

Qu'est ce qu'est un prédicat ?

Le concept de prédicat représente le concept de proposition, exprimé de manière plus générale. En effet, un prédicat représente une information quelconque, comportant une valeur inconnue. Donc, en modifiant cette valeur inconnue par une valeur connue, vous obtenez une proposition précise. Il existe donc un ensemble de valeurs pour lequelle la proposition obtenue est vraie, et un autre ensemble de valeurs pour lequelle la proposition obtenue est fausse. Un prédicat est, en quelque sorte, une fonction prenant une valeur quelconque en entrée, et soit "vrai" soit "faux" en sortie.

Les axiomes du calcul propositionnel

Oui, même une branche mathématique aussi axée "logique" a des axiomes. En réalité, le calcul propositionnel a 4 axiomes consistant en 4 tautologies, extrêmement simples. Premièrement, "Si P OU P, Alors P". Deuxièmement, "Si P, Alors P OU Q". Troisièmement, "Si P OU Q, Alors Q OU P". Quatrièmement, "Si P IMPLIQUE Q, Alors Si P IMPLIQUE R Alors Q IMPLIQUE R". Aussi basiques qu'elles puissent être, en leur statut d'axiome, ces propositions sont indémontrée, mais toujours vraies. Cependant, on peut rajouter une règle d'interférence tout aussi évidente : le modus ponens. Le modus ponens énonce que "Si P IMPLIQUE Q, ET P Est Vrai, Q Est Vrai". Il représente une façon d'utiliser l'implication, utile par exemple lors d'une démonstration.

Utiliser les propositions et les prédicats

Le calcul propositionnel

L'idée avec ces propositions est de les assembler pour obtenir (de manière précise) toutes les opérations nécessaires à la démonstration d'une proposition, tout aussi complexe soit elle. Pour cela, il faut souvent utiliser plusieurs propositions assembler de manière très précise. Cette assemblage utilise son propre langage. Ici, les propositions utilisées sont nommées variables propositionnels (ou propositions atomiques). Il est possible de les lier entre elles, avec des connecteurs logiques. En fait, les connecteurs logiques permettent de créer des propositions plus complexes, avec une (ou plusieurs) autres expressions plus simples. Bien que ce concept puisse être compliqué, il s'agit en réalité de concepts assez simples. Par exemple, le "ET" logique permet de créer une expression avec deux autres expressions "p" et "q", vraie si "p" et "q" le sont aussi. Dans les connecteurs importants, ont peut aussi citer "OU", "NON" ou "IMPLIQUE".

Une autre utilité de ces concepts est la déduction mathématique. Comme vu auparavant, la déduction mathématique consiste à former un ensemble de propositions et connecteurs logiques, pour former des démonstrations concrètes. Le passage de l'un à l'autre est régit par une notation assez précise. Les propositions permettant la vérification de la conclusion sont nommées les prémisses. En calcul propositionnel, les règles à suivre pour former / déduire des propositions valides représentent ce que l'on appelle la syntaxe.

Bien évidemment, utiliser des propositions "p" et "q", c'est bien, mais extrêmement abstrait. Les méthodes d'attributions de propositions bien réelles à ces propositions abstraites représentent ce que l'on appelle la sémantique. Par exemple, en arithmétique, un nombre entier est pair si il peut s'écrire sous la forme "2 * k", avec "k" un entier quelconque. Définissons la proposition "p" tel que, pour un n quelconque, "n est pair". De plus, un nombre entier est impair si il peut s'écrire sous la forme "2 * k + 1", avec "k" un entier quelconque. Définissons la proposition "q" tel que "n est impair". Dans un cadre logique, la proposition "p ET q" énonce un "n" pair et impair, et donc "2 * k = 2 * l + 1". Or, selon les lois primaires de l'arithmétique, ce n'est pas possible, donc "p ET q" n'est jamais vraie dans ce contexte, mais "p ET NON q" (ou "NON p ET q") l'est toujours (de manière assez évidente). Il est possible de pousser le raisonnement plus loin pour plus de rigueur, mais le résultat est le même. Il est à noter que, dans le cas d'exemples aussi simples, les résultats obtenus sont particulièrement évidents (tellement qu'ils peuvent en sembler complexe à déduire). Les règles précises utilisées dans une sémantique sont définies dans ce que l'on appelle un modèle. Ces modèles permettent de définir des ensembles d'axiomes (et de propositions faites avec ces axiomes) nommés des théories axiomatiques (souvent abrégées en "théories").

Le calcul des prédicats

Bien évidemment, les prédicats obéissent aussi aux propriétés des propositions. Hors, ils peuvent aussi (dans un même modèle) avoir des valeurs différentes selon la valeur de leur inconnue. Pour bien les définir, il existe d'autres notions très similaires, pour bien spécifier l'opération actuelle nécessaire à l'étude. Pour commencer nous allons attribuer à chaque prédicat / fonction nécessaire un symbôle, nommé une signature. Ici, nous allons différencier les notions de prédicat et de fonction de manière assez simple : un prédicat retourne une valeur "vraie" ou "faux", et une fonction retourne une autre valeur, qui n'a pas vocation à être directement utilisée en tant que "vrai" ou "faux". D'un point de vue algébrique, nous pouvons donner à chaque prédicat / fonction une valeur représentant le nombre de termes nécessaires en entré, que nous appelons l'arité du prédicat / fonction. En suite, nous allons utiliser les valeurs avec les fonctions directement (et pas les prédicats), dans ce que l'on appelle un terme. Une valeur quelconque n'ayant pas besoin de fonction peut aussi représenter un terme. Finalement, nous allons placer plusieurs termes dans un prédicat général, pour former ce que l'on appelle une formule. Il est aussi possible de créer des formules via d'autres formules, en les interprétant directement comme des prédicats. Si une formule est vraie dans au moins un modèle, elle est dite satisfaisable, et si elle est vraie dans tous les modèles possibles, elle est dite "loi logique".

Dans une formule, l'interprétation en tant que prédicat nécessite de prendre en compte les inconnus nécessaires. Pour spécifier certaines valeurs d'inconnues, nous pouvons utiliser des objets nommés des quantificateurs. Il en existe deux principaux : "pour tout" désignant toutes les inconnues possibles, et "il existe" désignant au moins une (ou plusieurs) inconnue. Dans ce cas, l'inconnue est dite "liée" à la formule, et dans le cas contraire, elle est dite "libre". Si toutes les inconnues d'une formule sont liées, la formule est nommée un enoncé (c'est le cas de l'exemple en haut).

Cette même logique est particulièrement efficace, car elle est démontrée comme ayant des caractéristiques très pratiques. Déjà, le calcul des prédicats permet, selon le théorème de complétude de Godel, d'être sur que tout théorème (logiquement) vrai est démontrable (dans tous les modèles). Bien que cela puisse paraitre parfaitement évident, ce résultat permet de démontrer une certaine unicité logique dans les théories. Le calcul des prédicats admet aussi un théorème de compacité. En effet, si toutes les sous-parties quelconques d'une théorie axiomatique sont satisfaisables, alors la théorie entière l'est aussi.

Qu'est ce qu'est la théorie des ensembles ?

La base de la théorie

L'idée de la théorie des ensembles, comme introduite par Georg Cantor à la fin du 19ème siècle, est de proposer un fondement solide aux mathématiques. Elle représente l'étude d'objets mathématiques, nommés des ensembles. De manière parfaitement intuitive, un ensemble représente un... ensemble d'éléments. Si un élément se trouve dans un ensemble, on dit que cet élément appartient à l'ensemble : c'est la relation (élément - ensemble) d'appartenance. Cependant, il est aussi possible de définir un ensemble sans aucun élément, nommée un ensemble vide. De plus, dans certains cas, un objet ressemblant à un ensemble (contenant d'autres objets mathématiques) ne peut pas appartenir à un autre ensemble : il s'agit dans ce cas d'une classe.

Nous pouvons faire pas mal d'opérations basiques avec ces ensembles. Si TOUS les éléments d'un ensemble A appartiennent à un autre ensemble B, alors on dit que A est inclu dans B. La réciproque n'est pas vraie : l'ensemble des nombres premiers est inclu dans l'ensemble des nombres (tous les nombres premiers sont des nombres), mais l'ensemble des nombres n'est pas inclu dans l'ensemble des nombres premiers (8 est un nombre, mais n'est pas premier). Dans ce cas, nous pouvons dire que A est un sous-ensemble (ou une partie) de A. D'ailleurs, il ne faut pas confondre l'inclusion et l'appartenance : un élément appartient à un ensemble, et un ensemble est inclu dans un autre ensemble (ils partagent des éléments en commun).

En théorie des ensembles, l'axiomatisation la plus utilisée est l'axiomatisation Zermelo - Fraenkel; abrégée axiomatisation ZF. Commençons par les axiomes de Zermelo. Le premier axiome, l'axiome d'extensionnalité, dit que, si deux ensembles ont les mêmes éléments, ils sont égaux. Cet axiome assure l'unicité des ensembles. Le deuxième axiome, l'axiome de paire, indique que l'union des éléments de plusieurs ensembles ne peut contenir un élément x si (et seulement si) x est contenu dans au moins l'un des ensembles formant la paire. Il implique que la paire de plusieurs ensembles est unique et existe toujours. Le troisième axiome, l'axiome de la réunion, dit que, pour tous ensembles A constitué intégralement d'ensembles (un ensemble d'ensemble), il existe un autre ensemble contenant l'union des éléments tous les ensembles contenus dans A. Si vous n'avez pas compris, nous vous encourageons à relire cette phrase lentement, et faire un schéma en même temps (le plus dur est de comprendre la phrase, le concept est tout à fait évident). Le quatrième axiome, l'axiome de l'ensemble de paires, dit que, pour un ensemble A, il est possible de représenter TOUS les sous-ensembles possibles de A dans un autre ensemble. Le cinquième axiome, l'axiome de l'infini, assure qu'il est toujours possible d'obtenir une suite d'ensemble pouvant être représente comme la suite des entiers naturels. En gros, on permet l'existence d'un ensemble correspondant parfaitement à celui des entiers naturels. Finalement, le dernier axiome, le schéma d'axiome de compréhension, admet que pour un ensemble E et une propriété P pouvant être appliquée sur certains éléments de E, il existe un sous-ensemble de E tel que ses éléments respectent P. Cependant, ces axiomes sont insuffisants, et il faut en rajouter quelques-uns pour compléter la théorie. En effet, nous allons généraliser le schéma d'axiome de compréhension si P est une transformation, en admettant l'existence d'un ensemble F, représentant les images (possibles) des valeurs de E après P. On peut aussi rajouter l'axiome de fondation, garantissant qu'un ensemble E ne peut pas appartenir à un autre ensemble F si E et F ont des éléments (généralement des ensembles) en commun. Cet axiome permet de dire qu'un ensemble ne peut pas appartenir à lui même, ou à une suite d'ensembles le possédant. Un dernier axiome (indépendant des autres) est l'axiome du choix. L'axiome du choix indique qu'il est possible de construire un ensemble à partir de pleins d'autres ensembles X, auquel on choisit un élément (par ensemble) grâce à une fonction quelconque (préalablement définie ou non) nommée fonction de choix. Cet axiome n'est pas toujours nécessaire.

Les ensembles

Les ensembles ont beaucoup de propriétés très intéressantes. Si les éléments d'un ensemble sont tous comparables entre eux, l'ensemble est dit ordonné : il s'agit d'une relation dite "d'ordre total" sur l'ensemble. Dans certains cas (mais pas tous), un ensemble peut avoir un plus petit élément : il est dit bien ordonné. Ce système de comparaison implique un ordre précis, et distinguable par une syntaxe. Si nous pouvons positionner les éléments d'un ensemble bien ordonné via une suite de nombres entiers naturels finie, alors l'ensemble est dit cardinal. De plus, le terme "cardinal" d'un ensemble est aussi utilisé pour désigner le nombres d'éléments présents dans cet ensemble. D'ailleurs, ce nombre peut être infini : on parle d'infini dénombrable (l'infini des nombres naturels), noté ℵ0. Ici, nous utilisons l'opération "positionner les éléments d'un ensemble bien ordonné via une suite de nombres entiers naturels finie" : cela équivaut à dire que nous attribuons à chaque élément d'un ensemble un unique nombre entier naturel. Cela représente une relation précise : l'équipotence. En effet, deux ensembles A et B sont équipotents si il est possible de lier chaque éléments de A à un unique élément de B (et inversement)(c'est une bijection d'ensemble). En toute logique, A et B ont donc le même cardinal. Cela peut créer certaines idées bizarres avec des ensembles infinis (à noter que, dans ces ensembles, le concept de taille d'ensemble ne veut plus rien dire). Par exemple, l'ensemble des entiers naturels est équipotent à l'ensemble des entiers naturels privés de 0. En effet, la bijection existe : elle est représentable par la fonction f(x) qui, a tout x appartenant à l'ensemble des entiers naturels, correspond un unique y tel que y = x + 1 : il y a un lien, et donc une équipotence. Avec cette opération, on peut en déduire que les ensembles (infinis) de nombres entiers naturels, entiers relatifs et nombres rationnels ont le même cardinal (l'ensemble des nombres réels n'a pas le même). Ces 4 résultats sont démontrés plus bas. De manière très (voir même trop) vulgarisée : infini + 1 = infini.

Cependant, certains types de comparaisons (défini par l'algèbre des éléments de l'ensemble) combiné à la définition de l'ensemble nécessitent un système de syntaxe particulièrement complexe. Par exemple, dans le cas d'un ensemble infini de couples (x, y), on définit la comparaison de ses couples comme la comparaison de x, puis y. Donc, (1, 0) > (0, 10) et (2, 4) < (3, 1). Or, si x est infini, alors le tri sera compliqué, puisque n'importe quel couple de position un nombre entier sera inférieur à (1, 0), ce qui n'est pas très pratique. Pour cela, la position x représentera un multiple d'une valeur "ω" de la position du couple. Donc, la position de (4, 0) sera 4ω, celle de (2, 3) sera de 2ω + 3 et celle de (0, 8) sera 8. Pour faire le lien avec la notion de cardinal vue plus bas, ω peut représenter le cardinal de l'ensemble (infini) des entiers naturels. L'addition "ω + x" représente donc "x valeurs après la dernière valeur de (0, a) avec a infini", soit (1, 0). D'ailleurs, si nous avons à étudier des triplets (x, y, z), alors la position d'un triplet serait "xω² + yω + z". Dans ce cas là, l'ensemble est dit ordinal. L'adaptation de ce que représente le multiple de ω dépend du contexte actuel dans lequel le nombre est utilisé (ici, un exemple évident avec des couples est utilisé).

Les opérations ensemblistes

Les applications mathématiques

En mathématiques, une application est une relation / lien entre deux ensembles. Pour être précis, une application relie un élément d'un ensemble vers un (unique) élément d'un autre ensemble. On appelle "image" un élément du premier ensemble, nommé ensemble de départ, et "antécédent" un élément du deuxième ensemble, nommé ensemble d'arrivée. Tous les éléments de l'ensemble de départ doivent être liés, mais pas forcément tous les éléments de l'ensemble d'arrivée. Pour définir correctement ce terme, on doit créer une structure contenant l'ensemble de départ, l'ensemble d'arrivée, et tous les liens entre chaque éléments de ces ensembles. Si les ensembles de départ et d'arrivée peuvent être définis dans des structures algébriques, alors nous pouvons utiliser le terme de morphisme de structures algébriques. Dans certains cas, une application peut avoir besoin de plusieurs antécédents, pouvant être contradictoire avec la définition : il faut garder en tête que l'ensemble de départ peut être le produit carthésien de tous les ensembles dans lesquels les antécédents sont contenus, annulant la contradiction.

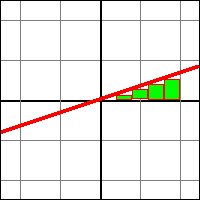
Ce terme est souvent confondu avec celui de fonction. En réalité, une fonction représente une application, où il est possible qu'un élément de l'ensemble de départ n'ait pas d'image. En général, le terme de fonction est utilisé dans le cadre de nombres numérique (ou d'ensembles de nombres numériques). Il est aussi très commun de définir une fonction avec la transformation associée à cette fonction, nommée l'expression de la fonction (par exemple "3x + 2"). Cependant, dans les deux cas, ce n'est pas obligatoire de fournir une expression (bien que très abstrait).

Il est possible de représenter des applications de pleins de façons possibles. La forme la plus connues pour les fonctions numériques est le graphe d'application (ou graphe de fonction, si l'on parle de fonction). Le graphe d'application numérique est une représentation graphique présentant les liens entre l'ensemble de définition est l'ensemble d'arrivée. Dans le cas de nombre seul (comme pour l'ensemble des réels), on représente en abscisse et en ordonné la droite des réels, et on note les points où le lien entre éléments a lieu. C'est... la façon compliquée de définir une fonction tracée dans un graphique.

Selon la façon dont son formés les liens, l'application peut avoir plusieurs propriétés intéressantes. Si chaque antécédent admet au maximum 1 antécédent, la fonction est dite injective. Tous les antécédents ont donc des images différentes, mais pas toutes les images ont forcément un antécédent. Si chaque antécédent admet au minimum 1 antécédent, la fonction est dite surjective. Ici, deux antécédents peuvent avoir la même image. Finalement, si chaque antécédent admet exactement une image, la fonction est dite bijective. C'est un renforcement de l'injectivité : toutes les images ont ici un antécédent. D'ailleurs, dans ce cas là, il existe une application inverse, avec comme ensemble de départ l'ensemble d'arrivée de l'application de départ, et comme ensemble d'arrivée l'ensemble de départ de l'application de départ. Les liens, eux, ne changent pas. Cette application est dite réciproque à l'application de départ.

Catégoriser les objets

Les structures mathématiques

En mathématiques, il est difficile de trouver une définition globale des structures mathématiques, objets étudiés par la théorie des catégories. Disons qu'une structure mathématique est une extension de la notion d'ensemble (ou de classe), en définissant avec cette ensemble des relations / opérations et axiomesprécis. Ici, l'ensemble peut être n'importe lequel, comme l'ensemble des nombres entiers naturels, et les "relations et axiomes" peuvent aussi être n'importe lesquelles, comme l'opération d'addition ou les axiomes de Peano (axiomes de bases de l'arithmétique). Si nous définissons des règles opératoires en plus de notre ensemble, nous parlons de structure algébrique(corps, groupes...).

Lier différents concepts

Certaines structures mathématiques distinctes peuvent avoir des points communs très prononcés. La théorie des catégories étudie les liens possibles entre certaines structures logiquement très semblables. En toute logique, une catégorie est donc la description de l'ensemble des structures respectant certaines propriétés précises. Elle est donc le socle de toutes les théories similaires nécessitant de passer d'une structure à une autre, comme la théorie des groupes et les éléments associés (une structure est appelée un groupe si elle a une structure de groupe : une opération interne additive, avec élément neutre et opposé).

Les morphismes

Le lien (qui n'est pas toujours une application) entre deux structures algébriques gardant ce genre de propriété est nommée un morphisme. Bien que la relation entre les deux structures ne soient pas toujours une application, la relation entre les ensembles constituant les structures en est bien une (et peut donc aussi être une fonction). Par exemple, une fonction définie sur l'ensemble des réels et arrivant sur l'ensemble des réels transforme la droite des réels en une nouvelle droite décrite par la fonction (morphisme d'un corps de réel vers... un corps de réel). Cependant, ce terme est un peu lourd pour l'utiliser avec celui de fonction.

Utiliser la logique en mathématique

Les théories axiomatiques

Avant de créer un modèle, il faut une base où construire notre modèle : cette base représente les théories axiomatiques. En mathématique, une théorie axiomatique représente une structure mathématique, composée d'axiomes et des théorèmes obstensibles via ces axiomes. Le plus dur ici est de trouver ces théorèmes.

Qu'est ce qu'est la théorie des modèles ?

Devoir créer une syntaxe précise pour chaque théorie mathématique est très long, et peut intéressant. Heuresement, la théorie des modèles est là pour aider. En fait, la théorie des modèles permet de faire un lien entre des "formes" syntaxiques provenant de la logique formelle, et les théories axiomatiques, permettant de déruire les théorèmes. Elles permettent, via la syntaxe logique, de donner un "sens précis" à la théorie, nommé la sémantique.

Pour un concept aussi abstrait, un exemple s'impose. Prenons une proposition quelconque du calcul des prédicats. Pour rappel, une notation comme celle-ci se nomme une formule.

Ici, nous allons utiliser une thérie axiomatique simple pour utiliser cette expression, par exemple l'arithmétique (de Peano). Pour cela, nous allons définir des valeurs précises à P et Q, qui peuvent être soit "vrai", soit "faux" : nous appelons ça des valeurs de vérités. Ici, P et Q doivent être des formules atomiques (elle ne peuvent pas être décomposés en formules plus petites). Ces mêmes formules reposent en général sur un ensemble d'objets élémentaires, nommé un domaine (si il est infini, le modèle est aussi appelé infini). Disons que P représente la proposition "tout nombre premier x est impair" et Q représente la proposition "tout nombre impair a un reste de 1 via la division par 2". Dans notre cas, le domaine représente l'ensemble des nombres premiers. Vous pouvez y utiliser des règles logiques parfaitement évidentes, comme le modus ponen.

De manière parfaitement évident, si un nombre est premier, il est impair. En quelque sorte, il s'agit d'un théorème mathématique, faisant partie d'une théorie mathématique. En prenant d'autres formules (plus intéressantes), vous pouvez démontrer pleins de choses très pratiques. Pour être plus précis, un modèle mathématique représente un ensemble de formules, composé de toutes les formules démontrables dans la théorie axiomatique. Vous pouvez piocher dans ce même modèle des formules permettant de démontrer un théorème de votre théorie axiomatique.

Certaines formules utilisent des propriétés hors du cadre logique de la théorie axiomatique utilisée : elle ne sont valables nulle part dans la théorie. Cependant, certaines formules peuvent très bien s'écrire, et être vrai ou fausse. Si une formule est vraie dans au moins un modèle de la théorie, la formule est dite satisfaisable. De manière similaire, une théorie est satisfaisable si elle admet au moins un modèle où tous ces axiomes sont vrais en même temps (si ils ne le sont pas, la théorie ne sert à rien). À l'inverse, il existe un théorème qui explique que, si un théorème existe via une formule dans un modèle d'une théorie axiomatique, alors on peut décortiquer la formule pour trouver la démonstration via les axiomes / autres théorèmes de la théorie : c'est le théorème de complétude de Godel. Aussi évident soit ce théorème, il est la base d'une grande partie de la déduction logique en mathématique. De plus, la théorie est dite cohérente si elle ne contient aucune contradiction. D'un point de vu sémantique, cela revient à dire que la théorie admet au moins un modèle. D'un point de vu syntaxique, cela revient à dire que la théorie ne prouve pas en même temps un théorème et sa contradiction. Cela implique que certaines formules existantes (les formules contradictoires des formules déjà prouvées) ne sont pas prouvables dans la théorie.

Il existe un théorème assez important dans cette théorie : le théorème de Löwenheim-Skolem. Selon ce théorème, si une théorie admet un modèle infini, alors elle admet aussi un modèle infini à cardinalité supérieure. Dans le cas de l'arithmétique de Peano, on peut démontrer qu'il existe des modèles infinis à cardinalité indénombrable (il ne sont cependant pas considérés comme "classique", et leur étude revient au cadre de l'algèbre non-classique). De manière simplifié, ce théorème consiste à dire que, si une formule est vraie dans un modèle, alors elle peut l'être dans d'autres (assez évident).