Les fonctions

Les fonctions représentent un moyen de lier un objet mathématique (appelé ici antécédent, ou variables) avec une transformation de ce dernier, et d'étudier l'objet transformé (appelée image). Tous les objets transformables de la fonction sont définis dans un ensemble, nommé ensemble de définition. En général, cet ensemble est composé de nombres, mais il est aussi possible qu'une fonction puisse prendre n'importe quelle autre type de valeur. De plus, une fonction peut prendre 1 seul antécédent, ou plusieurs antécédents. De même manière, une fonction peut transformer ses antécédents en 1 ou plusieurs images. L'ensemble de toutes les valeurs obtensibles via une fonction est nommé l'ensemble d'arrivée de la fonction.

Comme tout objets mathématiques, elle a un nom, et tout un système de notation dédié pour les utiliser. Par exemple, définissons une fonction "f" prenant un antécédent "x" défini sur l'ensemble "E". Une image "i" de "f" pour un certain "x" s'écrit :

$\mathrm{f(x)}=i$

Cependant, quand on connait la fonction, le plus utile est d'indiquer la transformation qu'effectue "f" pour "x", appelée l'expression de la fonction :

$\mathrm{f(x)}=3*x+2$

L'avantage de l'utilisation des fonctions est la possibilité de généraliser certaines transformations mathématiques, et de les étudier plus facilement.

Dans le cas des fonctions numériques, il existe beaucoup de formes possibles. Les plus connues sont les polynômes.

$\mathrm{f(x)}=\mathrm{ax}$

Une opération de calcul infinitésimal

La défintion, via un graphique

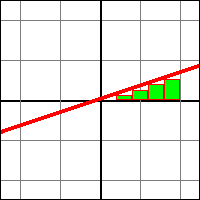
Pour une fonction continue prenant un inconnu, on peut tracer sa représentation sur un graphique. Dans ce même graphique, l'aire entre la droite des abscisses et la courbe tracé par la fonction "f" entre deux absisse "a" et "b" est nommée "intégrale de f entre a et b". Pour obtenir cette aire, on peut définir "n" rectangles entre la courbe et la droite des abscisses, et obtenir une approximation de l'aire avec la somme de l'aire de ces rectangles.

Le théorème fondamental de l'analyse

Le théorème fondamental de l'analyse, démontré par (entre autre) Isaac Newton, affirme que l'intégrale d'une fonction peut s'obtenir avec sa primitive. En réalité, l'intégrale de la fonction "f" entre "a" et "b" est une fonction primitive de "f" (idéalement, s'annulant en "a") à la valeur "b", auquelle on enlève une valeur constante (qui dépend de la primitive utilisée). Cette constante est dû au fait que une fonction a une infinité de primitives, avec une seule correspondant exactement à son intégrale (et les autres devant être corrigés par une valeur constante). Donc, cela équivaut à dire que l'intégrale de la fonction "f" entre "a" et "b" est la différence entre la primitive généralisée de "f" pour b et la primitive généralisée de "f" pour a.

$\mathrm{F(x)}=\mathrm{f(t)dt}$

D'un point de vue "épistémologique", ce théorème est parfaitement logique. En effet, le nombre dérivé d'une valeur de fonction est la variation infinitésimal de la fonction à cette valeur. Pour rappel, une variation infinitésimal de la fonction de départ fait... varier la fonction de départ. En toute logique, l'obstention d'une fonction par sa dérivée se fait en appliquant toutes les valeurs de la dérivée en tant que variation infinitésimale de la fonction. Donc, la primitive d'une fonction en "x" représente la somme infinitésimale de toutes les valeurs précédentes de "x" dans la fonction, interprétées comme variations de la primitive. On peut représenter ces valeurs infinitésimals comme l'aire précise sous cette valeur de la fonction (de largeur infinitésimale). Donc, la primitive d'une fonction représente la somme de toutes ces aires, et donc l'intégrale (aire sous la courbe) de la fonction.

Ce théorème permet de démontrer rigoureusement pleins de propriétés (en réalité, assez triviales). Par exemple, les intégrales peuvent se calculer avec la relation de Chasles.

$\int x_y^{}f(t)dt+\int y_z^{}f(t)dt=\int x_z^{}f(t)dt$

Il est aussi possible de découper des intégrales pour calculer ces parties dans des intégrales différentes (et plus simple). Ce concept s'appelle l'intégration par partie.

$\int x_y^{}u(t)*v\text{'}(t)dt=\mathrm{[u(t)*v(t)]}{x}_y^{}-\int x_y^{}u\text{'}(t)*v(t)dt$

Qu'est ce qu'est la fonction exponentielle ?

La définition brute

En analyse fonctionelle réelle, la fonction exponentielle est une fonction n'ayant qu'une seule dérivée : elle même. Cette fonction est assez facilement déductible avec des équations différentielles. En gros, en cherchant une valeur commune aux tengantes de cette fonction, on remarque que cette fonction, n'ayant qu'une seule dérivée (elle même), est un nombre élevé à la puissance x. Ce nombre est appelé nombre exponentiel, est appelé "e" (ou nombre d'Euler), et vaut approximativement 2,71828. Elle est continue et dérivable sur R. Donc, pour tout x appartenant à R :

$\mathrm{exp(x)}=e^x|\mathrm{exp\text{'}(x)}=\mathrm{exp(x)}=e^x$

Cependant, le nom "fonction exponentielle" peut aussi désigner des fonctions similaires, mais pas exactement égales à la fonction que nous venons de voir. En effet, une fonction exponentielle peut être n'importe qu'elle fonction suivant cette forme:

$\mathrm{exp(x)}={\mathrm{ae}}^{\mathrm{bx}}$

Les logarithmes

La fonction réciproque de la fonction exponentielle est nommée la fonction logarithme. Elle permet de faire le lien entre la valeur d'une puissance et la puissance utilisé. D'un point de vu mathématique :

$\mathrm{exp(log(x))}=e^{\mathrm{log(x)}}=x$

Grâce aux propriétés de l'exponentiel, on peut généraliser pour n'importe quelle valeur.