Logo de SAASF

Le chapitre 2

Contenu

L'algèbre en mathématiques

La discipline du calcul mathématique

Qu'est ce qu'est le calcul

Commençons par le commencement, avec des définitions pures. En mathématiques, un calcul est une suite d'actions qui permettent de passer d'une forme quelconque à une autre. La branche la plus simple du calcul est le calcul numérique. Un calcul est dit numérique quand il ne permet de travailler que sur des nombres connus. Par exemple, un calcul permet de faire ceci :

(3 +(4 * 2)) - 5 =6

Avec ce calcul, les règles permettant de définir les actions possibles sont en général les règles très basiques vues au début de l'enseignement scolaire.

Qu'est ce qu'est l'algèbre classique ?

En mathématiques, l'algèbre classique est la discipline mathématique qui étudie le concept brut de calcul algébrique. En fait, un calcul est une suite d'actions qui permettent de passer d'une forme quelconque à une autre. un calcul est dit algébrique si il permet de travailler avec des indéterminés. Le calcul algébrique est donc une extension du calcul numérique. Les actions possibles sur ces formes sont définis de manière "axiomatique" par l'algèbre classique. En réalité, ces axiomes ne le sont que par le point de vue de la théorie, mais sont déductibles d'autres théories plus complexes (que nous verrons après). Par exemple, avec des nombres entiers, une des actions possibles est de faire ça :

a * (b +c) =a * b +a * c

D'un point de vue logique, on peut quantifier cette action pour en faire une proposition toujours vraie.

∀a,b,c ∈N,a * (b +c) =a * b +a * c

Qu'est ce qu'est l'algèbre générale ?

Si il y a une algèbre "classique", il y a une algèbre "générale". En mathématiques, l'algèbre générale est la discipline mathématique qui étudie les différentes formes d'algèbres classiques possibles, sous forme de structures algébriques. Une structure algébrique est la mise en commun d'un ensemble et d'une (ou plusieurs) opération de calcul (nommées "lois de composition internes"), pour les étudier de manière conjointe. En fait, chaque structure algébrique possède ses propres propriétés de calcul, avec les opérations décrites dans la structure. C'est grâce à cela que nous savons comment obtenir les "axiomes" de l'algèbre classique, ou même du calcul numérique.

Les structures algébriques et lois de compositions

Pour rappel, une structure algébrique est la mise en commun d'un ensemble et d'une (ou plusieurs) opération de calcul (nommées "lois de composition internes"), pour les étudier de manière conjointe. Hors, utiliser le terme "opération" est, comme nous l'avons déjà dit au dernier chapitre, ambiguë : nous allons le remplacer par le terme "loi de composition". Une loi de composition est une application entre tous les éléments de deux ensembles "A" et "B", et vers des éléments de "A". Il s'agit d'un type précis d'opération binaire, avec au moins un opérande étant du même ensemble que le résultat. De manière plus rigoureuse (et mathématique) : une loi de composition est une application entre tous les éléments du produit cartésien de deux ensembles "A" et "B" (ou du produit cartésien de "B" et "A"), et vers des éléments de "A". Parmi tout ce que l'on a vue, nous avons vu une loi de composition : l'addition (de "N X N" vers "N"). Voici un tableau représentant à l'horizontal le premier opérande, à la vertical le deuxième opérande et leur résultat lors de leur croisement.

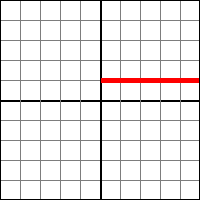
Il y a une grosse différence entre la notion de loi de composition et la notion d'opération : la stabilité. Une opération entre plusieurs objets est dite stable (ou close) en un ensemble E si, pour tous les éléments possibles au départ, l'arrivée est toujours dans E. Si une opération binaire est stable et que au moins un de ces opérandes est du même ensemble que le résultat, alors elle est une loi de composition. Par exemple, l'opération addition entre deux nombres entiers naturels est stable dans les nombres entiers naturels (démontré au premier chapitre). Prenez n'importe quels nombres naturels et additionnez les : vous aurez toujours un nombre entier naturel. À l'inverse, l'opération soustraction entre deux nombres entiers naturels n'est pas stable dans les nombres entiers naturels, car il existe des contres-exemples (4 - 9 fait -5, qui n'est pas un nombre entier naturel). Voici un exemple légèrement plus complexe : l'opération d'addition de "{0, 1, 2, 3}" et "{0, 1, 2, 3}" (lui même) n'est pas stable dans "{0, 1, 2, 3}".

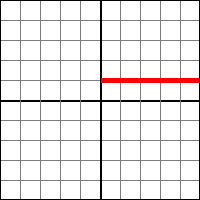
Le cas le plus utile est quand la loi de composition est dite interne. Une loi de composition est dite interne lorsque les deux éléments de départs sont les mêmes (et donc, les mêmes que l'ensemble d'arrivée aussi). Par exemple, c'est (encore) le cas de l'addition dans les nombres entiers naturels. Pour un ensemble E, une loi de composition interne "l" notée "." se définie comme ça :

l : E X E ⟶E
∀a,b ∈E,∃! c ∈E,a . b =c

Une manière intéressante d'étudier une loi de composition interne est la table de Cayley. Une table de Cayley est une représentation sous forme de tableau à deux entrées des valeurs obtenues grâce à une loi de composition entre chaque élément d'une structure algébrique finie. Nos exemples plus haut ne sont pas exactement des tables de Cayley, car l'ensemble "N" est infini (dans le premier cas), et la loi de composition n'est pas interne (dans le deuxième cas). En regardant précisément comment se comportent les éléments de la table, nous pouvons en déduire des propriétés plutôt intéressantes, sur dans des cas de structures très originales. Voici un exemple : la table de Cayley représentant l'ensemble des restes par la division euclidienne de nombres par 5 (après l'application de la loi de composition interne), avec comme loi de composition interne l'addition.

Les lois de compositions internes peuvent avoir une très grande quantité de propriété, très souvent syntaxiques (liée à la façon dont vous pouvez écrire avec la loi). La plus simple est l'associativité. Une loi de composition interne est dite associative si l'ordre de réalisation de plusieurs opérations ne modifie pas le résultat. En fait, si notre loi "." est associative, alors :

∀a,b,c ∈E,(a +b) +c =a +(b +c)

Comme nous l'avons démontré au chapitre précédent, l'addition et la multiplication sont associative. Cependant, la puissance n'est pas associative, et voici un contre exemple :

2 ^ (2 ^ 3) =2 ^ 8 =256
(2 ^ 2) ^ 3 =4 ^ 3 =64

Les lois de compositions internes peuvent aussi permettre l'existence d'éléments remarquables dans E (quand utilisés avec la loi). Le plus simple est l'élément neutre. Un élément est dit neutre par une loi de composition si l'utilisation de la loi sur un autre élément "a" et cet élément donne "a". Il ne modifie pas ce fameux élément "a", comme montré dans cette définition (ou "e" est l'élément neutre).

∀a ∈E,a +e =a

C'est, par exemple, le cas du "0" dans l'addition dans les nombres entiers naturels, ou de "1" dans la multiplication ou la puissance dans ce même ensemble.

∀a ∈E,a +0 =a
∀a ∈E,a * 1 =a

Il est à noter que, si une loi de composition commutative permet l'existence d'un élément neutre dans un ensemble, alors il n'y en a qu'un seul dans l'ensemble (démontré ici).

Maintenant, parlons des structures algébriques. Pour rappel, une structure algébrique est la mise en commun d'un ensemble et d'une (ou plusieurs) opération de calcul (nommées "lois de composition internes"), pour les étudier de manière conjointe. Nous avons donc besoin de deux objets : un ensemble "E", et une (ou des) opération ".". La notation pour une structure algébrique se note ainsi.

(E,.)

Dans un cas très simple, voici la structure algébrique correspondant à l'ensemble des nombres entiers naturels et de l'addition (dont on peut prouver facilement l'existence, comme ici) :

(N,+)

Les différents types de structures algébriques

Magmas et groupes

Les structures algébriques sont catégorisées par les propriétés des lois de compositions internes avec l'ensemble utilisé. Le type de structure algébrique le plus simple est le magma. En algèbre, un magma est une structure algébrique représentant un ensemble quelconque et une seule loi de composition interne sur cette ensemble, sans plus de détail. Bien que très générale, cette définition est très faible. Il existe une quantité aberrante de magma : (N, +), (N, *), (N, ^)... La seule chose à prouver pour que l'union d'un ensemble et d'une opération soit un magma et de prouver que l'opération est stable.

À l'inverse, une structure très utilisée est le groupe. En algèbre, un groupe est un magma dont la loi de composition interne et associative, admet un neutre, et est inversible. Bien que cette définition semble très générale, elle exclut directement tous les exemples vues plus tôt : (N, +) et (N, *) ne sont pas inversibles, et (N, ^) n'est même pas associative. Cependant, l'addition sur Z permet de former un groupe. D'ailleurs, les groupes utilisant comme loi de composition interne une forme "d'addition" sont dit additifs.

(Z,+)

Dans un groupe, l'inverse d'un élément "a" est généralement noté "a exposant -1". Cette notation peut être risquée si vous ne savez pas si vous travaillez avec un groupe, ou avec un nombre "normal" : faites donc toujours attention au contexte.

G =(E,¤),∀a ∈E,a¤ a-1=0G

Une catégorie de groupe plus forte est le groupe abélien. Un groupe est dit abélien si sa loi de composition est commutative. (Z, +) en est un exemple.

Les sous-groupes

Comme il exemple des sous-ensembles d'ensembles, il existe des sous-groupes de groupes. Ici, un sous-groupe H d'un groupe G est un groupe sur un sous-ensemble de l'ensemble de G, muni de la même loi de composition que G. Ce groupe doit donc contenir les mêmes propriétés que tous les groupes : stabilité de la loi, associativité, neutre et inversibilité. Déjà (et si la loi est stable), comme un sous-groupe est défini sur un sous-ensemble de son groupe de départ, alors les éléments du sous-groupe sont aussi dans ceux du groupe, et la condition d'associativité est toujours assurée (inutile de la démontrer à chaque fois).

∀a,b,c ∈E,(a . b) . c =a . (b . c)
⇒∀F ⊆E,∀a,b,c ∈F,[a,b,c ∈E] ⇔[(a . b) . c =a . (b . c)]

De plus (toujours si la loi est stable), prouver que ce sous-groupe possède un neutre revient à démontrer que le neutre du groupe de départ se situe dans le sous-ensemble. La démonstration de cette proposition est presque identique à celle pour l'associativité.

∀a ∈E,∃e ∈E,a . e =a
⇒∀F ⊆E,∀a ∈F,[a ∈E] ⇔[∃e ∈E,a . e =a]

Finalement, la seule difficulté est de prouver que la loi est stable sur l'ensemble du sous-groupe (et donc, sur le sous-ensemble de l'ensemble du groupe), et que chaque élément de l'ensemble du sous-groupe possède un inverse, toujours dans le sous-groupe. Pour avoir un exemple, prenons... un exemple. Imagineons le groupe "G" représentant le groupe additif des entiers relatifs.

G =(Z,+)

Prenons un sous ensemble de "Z" : l'ensemble des nombres pairs "2Z". Comme nous l'avons vue, les éléments de "2Z" représentent tous les multiples de 2. La question est donc simple : est-ce que le groupe additif sur "2Z" est un sous-groupe de "G"? Déjà, vérifions si "2Z" est stable sur l'addition.

∀a,b ∈2Z,∃c,d,e ∈Z,[a =2 * c,b =2 * d,a +b =e]
⇒e =a +b =2 * c +2 * d =2 * (c +d)
⇒∃f ∈Z,[f =c +d,e =2 * f] ⇒e ∈2Z

Comme nous le constatons, toute somme d'éléments de "2Z" forme un élément de "2Z". Maintenant, vérifions la présence de chaque opposé de chaque élément de "2Z".

∀a ∈2Z,∃b,c ∈Z,[a =2 * b,a +c =0]
⇒2 * b +c =0 ⇒2 * b =-c ⇒2 * -b =c ⇒c ∈2Z

Chaque élément possède bien un opposé, dans "2Z". Finalement, nous pouvons très facilement démontrer que le neutre de "(Z, +)", 0, appartient à "2Z", car "2 * 0 = 0". Donc, "2Z" est un sous-groupe de "G".

Les groupes symétriques

Un type de groupe un petit peu bizarre mais assez atypique est le groupe symétrique. Le groupe symétrique (ou groupe des permutations) d'un ensemble "E" est un groupe sur l'ensemble des permutations de "E", et utilisant comme loi de composition la composition de fonction. Cela est parfaitement possible. En effet, comme nous l'avons vue au chapitre 1, la composition de deux bijections donne une bijection, la composition de bijection est associative, la bijection identité représente le neutre, et chaque bijection possède une inverse (sa réciproque). Bien qu'il puisse être un peu bizarre, il s'agit bien d'un groupe. Généralement, on le note avec la lettre "S" et le nom de l'ensemble "E".

S(E)

Il existe un autre concept très proche (et très lié) à ces groupes symétriques : les groupes de permutations. Un groupe de permutation d'un ensemble "E" est un sous-groupe du groupe symétrique (aussi nommé groupe des permutations) de "E". Ce concept permet d'énoncer un théorème très pratique : le théorème de Cayley.

Les opérations sur les structures algébriques

Les parties génératrices et sous-groupes engendrés

Les sous-groupes engendrés sont des objets algébriques, très utilisés dans l'étude des groupes. En effet, un sous-groupe engendré d'une partie "F" d'un groupe "G" sur un ensemble "E" représente l'ensemble des éléments de "G" que nous pouvons obtenir avec seulement une répétition de la loi du groupe sur des éléments de cette partie "F" (et / ou de leurs inverses). Pour un groupe "G" utilisant l'ensemble "E" et la loi "¤", un sous-groupe "H" engendré par la partie "F" de "E" est un sous-groupe de "G" sur une partie "D" de "E", et le plus important est de définir "D". Cependant, la définition rigoureuse de "D" est un peu complexe. Pour une traduction mathématique - français, lisez "Soit un groupe G formé d'un ensemble E, et d'une loi ¤, et F une partie de F. H est un groupe formé d'un ensemble D et d'une loi ¤, et D représente l'ensemble des éléments x de E tel qu'il existe un nombre entier naturel n dont tous les nombres entiers naturels inférieurs peuvent [indexer un ensemble f d'éléments de F] et [indexer un ensemble a représentant soit 1, soit -1], et que x représente n utilisations de ¤ entre chaque [élément de f exposant a (représentant soit l'élément direct, soit l'inverse), selon l'indice actuel]".

G =(E,¤),F ⊆E,H =(D,¤)
D ={x ∈E | ∃n ∈N,∃(f1,f2,...,fn) ∈Fn,∃(a1,a2,...,an) ∈{1, -1}n,x =f1a1¤ f2a2¤ ... ¤ fnan)}

Dans cette définition, il n'est pas exclu que tous les éléments "f" soient... un même élément, comme que les appartitions de "a" représentent toutes 1 ou -1 (ici, exposant 1 ne change rien, et exposant -1 représente l'inverse). On peut facilement voir que "D" est une partie de "E" (confirmant que "H" est un sous-groupe de "G"), puisque (par définition) tous les éléments de "D" appartiennent aussi à "E". Il existe une notation pour ces fameux sous-groupes engendrés : un sous-groupe engendré par une partie "F" se note ainsi, avec des sortes de chevrons:

H =⟨F⟩

Les parties génératrices représentent des sous-groupes engendrés un peu spéciaux. En effet, une partie génératrice d'un groupe est une partie "F" d'une groupe "G" sur un ensemble "E" où le sous-groupe engendré par "F" représente l’entièreté de "G".

H =⟨F⟩=G

Les morphismes

Il est possible de faire des applications entre structures algébriques tout en gardant les propriétés de la structure, grâce à un concept assez pratique : les morphismes. Cet objet est assez complexe, car il représente un objet d'une autre théorie logique très complexe (la théorie des catégories), mais une version simplifiée existe pour l'algèbre. Dans cette "théorie des catégories", un morphisme de structures est une application entre deux ensembles de deux structures, où les lois sont compatibles entre elles après utilisation de l'application. Ici, "structure" représente n'importe quoi qui admet des lois quelconques. Dire que les lois doivent être "compatibles entre elles" représente la différence entre une application et un morphisme. Déjà, par définition, toutes les lois de notre deuxième structures doivent avoir les exacts mêmes propriétés que celles de notre première structure(les deux structures doivent appartenir à la même catégorie de structure). De plus, cela veut dire que l'utilisation de la loi du groupe d'arrivée sur des images du morphisme et égal à utiliser la loi de l'ensemble de départ sur les deux antécédents, puis d'en obtenir leur image (et qu'elle est similaire au résultat obtenu grâce à la loi de la structure d'arrivée, au début). Bien évidemment, il faut que toutes les lois des deux structures respectent cette compatibilité.

Dans notre cas, ces "structures" représentent des structures algébriques. Donc, en algèbre, un morphisme de structures algébriques est une application entre deux ensembles de deux structures algébriques, où l'on doit s'assurer que les lois de composition de la première structure ont les mêmes propriétés que les lois de composition de la deuxième structure après utilisation de l'application, et que les lois de composition sont compatibles entre elles après utilisation de l'application. Déjà, par définition, les deux structures algébriques doivent être les mêmes (groupe vers groupe, monoïde vers monoïde...). En plus, comme pour le cas général, l'utilisation des lois de composition du groupe d'arrivée sur des images du morphisme est égal à utiliser cette loi à des éléments de l'ensemble de départ sur les antécédent, puis d'en obtenir leur image (et qu'elle est similaire au résultat obtenu grâce à la loi de composition de la structure d'arrivée, audébut).

Le cas le plus simple est le morphisme de groupe. Un morphisme de groupe est un morphisme d'un groupe vers un autre groupe, où les lois de composition des deux groupes sont compatible entre elles. Pour un groupe "G" et "H" quelconque, un morphisme "f" se présente comme cela :

G =(E,.)
H =(F,*)
m : E ⟶F,x ⟶f(x)

Pour l'instant, il s'agit d'une application normale. Pour en faire un morphisme, il faut qu'elle vérifie cette propriété :

∀y,z ∈E,f(y . z) =f(y) * f(z)

C'est la mise en forme littérale de la "compatibilité" des deux groupes.

Contenu

L'arithmétique des nombres rationnels

Une nouvelle façon de voir les nombres

Qu'est ce qu'est un nombre rationnel ?

Au dernier chapitre, l'accent était mis sur les ensembles "N" et "Z". On n'a donc défini des nombres comme des éléments que l'on peut placer sur une ligne, à une certaine distance de 0.

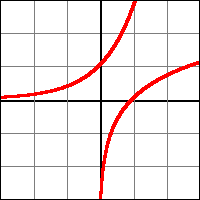
Avec les nombres rationnels, nous allons utiliser une catégorie différente de nombre. Déjà, nous allons considérer que chaque nombre entier est séparé par une distance précise, et que un nombre "n + 1" se trouve à une distance de "1" unité par rapport à "n". Ici, nous allons imaginer ces distances de manière géométrique, comme un trait entre "n" et "n + 1". Or, il est très facile d'obtenir le milieu de ce trait. Sur notre ligne, ce milieu ne correspond à aucun nombre entier. Or, nous savons que ce milieu se situant à une distance représentant la moitié de "1" existe. En fait, il est possible de représenter des distances coupées de cette manière, grâce à ces fameux nombres rationnels.

D'un point de vue rigoureux, un nombres rationnel représente un nombre entier relatif (nommé "numérateur"), que l'on a découpé (au sens de "diviser") en une quantité finie et non nulle (nommée "dénominateur"). La notion d'un nombre rationnel est inspirée de celle de la division (présentée dans le chapitre 1) : on note le numérateur au dessus du dénominateur, en les séparant par une barre (comme pour la division).

NumerateurDénominateur