Le chapitre 1

Le raisonnement mathématique

Le coeur des mathématiques

Le concept de proposition et d'inférence

Cette partie aura pour tâche de rappeler les concepts vus au chapitre 0 de ce cours. Pour cela, nous avons besoin de la définition des mathématiques et de la logique, que nous ne rappellerons pas ici.

En mathématiques, les informations que l'on cherche a démontrer sont formulées dans ce qui est nommé une "proposition". En effet, une proposition logique est une information quelconque, possédant une valeur de vérité (elle est soit vraie, soit fausse). En réalité, cette définition peut s'appliquer à d'autres mots, qui représentent le même objet (tournée de manière plus ou moins similaire) : assertion, énoncé, question... D'un point de vue vocabulaire, il existe pas mal de noms pour des propositions spéciales. Par exemple, une tautologie est une proposition qui est tout le temps vraie(comme la proposition "si je peux m'acheter à manger, alors j'ai de l'argent", qui est vraie dans tous les contextes). À l'inverse, une contradiction logique est une proposition logique toujours fausse(comme la proposition "si je n'ai pas accès à de l'argent, alors je peux acheter à manger", qui est fausse dans tous les contextes). Théoriquement, il est possible de considérer tout ce qui a une valeur de vérité comme une proposition.

En pratique, les propositions suivent une syntaxe assez précise, et assez claire. Pour rappel, une syntaxe représente les règles qui doivent suivre des mots (ou n'importe quel objet qu'on peut "écrire") rendant une phrase correcte. L'objet principal utilisé en syntaxe est la formule. En effet, une formule syntaxique représente un objet "écrit" quelconque obéissant à une syntaxe. L'exemple le plus simple de syntaxe est la langue française, où toutes les phrases possibles représentent des formules différentes. C'est la même chose pour les propositions (et pour tout ce qui englobe la logique), ou même les nombres. En fait, il faut comprendre que la syntaxe des propositions est très proche de la syntaxe des nombres. Par exemple, imaginez que vous travaillez sur la proposition "je suis un majeur". Vous pouvez la réécrire en entier partout, mais vous allez perdre du temps. Or, il est possible "d'enfermer" cette proposition sous la forme d'une "variable", comme avec les nombres. En d'autres termes, vous pouvez sans soucis écrire cette proposition sous la forme d'une variable "P", que vous pouvez utiliser comme si elle représenter la phrase entière :

P = "je suis un majeur"

Cependant, utiliser l'égalité en logique est peu recommander. En effet, dans notre exemple, on dit que "P" est forcément égal à la proposition "je suis majeur". Or, imaginez la proposition "Q" égal à la phrase "je remplis toutes les conditions nécessaires pour être majeur". Dans les deux cas, vous êtes majeur, mais "P" ne s'écrit pas comme "Q". Si "P" ne s'écrit pas exactement comme "Q", alors "P" n'est pas égale à "Q". Or, elles ont le même sens, on peut donc se demander si il existe un symbole remplaçant l'égalité, mais n'agissant que sur le sens de la proposition. Ce symbôle existe : il s'agit du symbôle "équivaut"(que nous ré-étudierons plus tard), et qui s'écrit comme ceci :

"Je suis un majeur" \Leftrightarrow "je remplis toutes les conditions nécessaires pour être majeur"

P \Leftrightarrow Q

Des fois, ce concept de "variable" est utilisé sans expliciter précisément la valeur de la proposition P : c'est normal. En effet, il est possible d'utiliser des propositions quelconques (et non explicitement définies) grâce à ces variables. Dans ce cas, des informations sont données sur ces propositions pour travailler avec. Ne soyez donc pas surpris si des propositions nommées "A", "B" ou même "P" se baladent toutes seules, sans être explicitées.

En parlant de syntaxe, parlons d'un sujet assez important pour comprendre les énoncés : les parenthèses. En fait, les parenthèses sont utilisées en mathématiques pour indiquer qu'une certaine partie d'une énoncé (la partie entre parenthèse) doit être traitées en priorité et en un bloc. Par exemple, dans le calcul "(3 + 2) * 3", les parenthèses nous permettent de savoir qu'il faut faire le calcul "3 + 2" avant la multiplication par 3. Or, on peut se retrouver dans des cas un peu plus complexes, comme "((3 + 2) * 4 + 8) / ((7 + 8) * (2 - 4))". Dans ce cas, pour ne pas se perdre dans les parenthèses, on peut utiliser des crochets / accolades à la place de certaines paires de parenthèses dans l'énoncé. Dans ce cas, "[(3 + 2) * 4 + 8] / [(7 + 8) * (2 - 4)]" est tout à fait valide (et plus simple à écrire).

Pour trouver correctement la valeur de vérité d'une proposition, il faut s'y prendre... correctement. La façon la plus utilisée est un procédé nommé l'inférence. Une inférence est une façon de démontrer logiquement une proposition (nommée "conclusion"), en s'appuyant sur d'autres propositions appelées "prémisses". Aussi effrayante que semble être cette définition, c'est en réalité très simple, et en voici un exemple (probablement le plus connu). Nous avons deux propositions de bases : "tous les hommes sont mortels" et "Socrate est un homme". Ici, une inférence consiste à dire que "Socrate est un homme, DONC il est mortel", aussi simple que ça. Socrate est utilisé dans l'exemple car il est l'une des grandes inspirations du concept (avec entre autres Aristote, Platon...). L'écriture mathématique actuelle (simplifiée) consiste en quelque chose comme ça :

A \Rightarrow B ET A DONC B

Les théories mathématiques

Plus haut dans ce cours, nous avons vu le concept de "syntaxe", cependant ce concept ne sert pas à grand chose sans son plus fidèle allié : la sémantique. La sémantique représente un moyen de donner un sens à une proposition énoncé grâce à une syntaxe. En linguistique, ce terme est particulièrement complexe, mais il est bien plus simple en mathématiques. En effet, le "sens" donner aux propositions représente tout simplement leurs valeur de vérité (vraie ou fausse). Dans ce cas, ces propositions deviennent des théorèmes. Cette définition regroupe un grand nombre de concepts : axiomes, inférences, modèle...

Pour déduire des théorèmes, il faut (comme nous l'avons vu) des propositions "de départs" nommées des axiomes. Pour rappel, les axiomes sont des propositions théoriquement indémontrées (mais qui, en pratique, sont tout à fait """"logiques""""" / évidentes, en accord avec les autres sciences et ne nécessitent pas de démonstration) qui servent de bases à toutes les mathématiques. Cependant, il existe un moyen de créer une quantité "infinie" d'axiomes, en définissant un plan pour définir cette quantité infinie d'axiome : les schémas d'axiomes. Les schémas d'axiomes sont un moyen de définir un "plan" (ou un schéma) pour créer une quantité infinie d'axiome. Cependant, une question peut se poser : pourquoi n'est-il pas possible de formuler ces fameux "schéma" sous la forme d'un seul et unique axiome ? En fait, un axiome ne peut pas utiliser directement dans sa formulation l'ensemble des propositions déduites de cette théorie. Cependant, certaines théories nécessitent que des axiomes puissent utiliser toutes ces autres propositions, démontrées avec les autres axiomes: ce concept est là pour ça. Il est à noter que ce concept est extrêmement abstrait : nous en présenterons des exemples clairs dans quelques lignes.

Maintenant, faisons un rappel sur les théories en mathématiques. Pour rappel, une théorie axiomatique est un ensemble d'axiomes, permettant de déduire / démontrer énormément de propositions (incluses dans la théorie). Avant de parler de la théorie axiomatique la plus importante (que nous présenterons dans la suite de ce cours), présentons quelques propriétés importantes sur les théories axiomatiques. Déjà, une théorie axiomatique est dite cohérente (ou consistante) si elle ne permet pas de prouver une proposition et sa négation. En logique classique, si "A" est vrai, alors il ne peut pas être faux (parfaitement évident, principe nommé "tiers exclu"). Cependant, si la théorie dit que "A" est vrai et fausse en même temps, elle est incohérente. C'est comme dire que quelqu'un est un majeur et un mineur en même temps : ça n'a pas de sens, et est impossible (et si une théorie / quelqu'un affirme le contraire, alors il est probablement fou). En général, on ne croise jamais de théorie non-cohérente, car elles sont abandonnées à la première incohérence trouvée.

En général, trouver une incohérence dans une théorie se fait en trouvant ce que l'on appelle un paradoxe. Selon l'Académie Française, un paradoxe logique est une (ou un ensemble de) proposition logique qui semble fonctionnel, mais comporte une contradiction logique (ou qui semble non-fonctionnel, mais l'est bel et bien). Cette définition s'applique à la littérature comme aux mathématiques. Un exemple assez connu est le paradoxe du fromage à trou : "plus on a de fromage avec des trous, plus il y a de trous". Or, "plus il y a de trous, moins il y a de fromages" : "plus il y a de fromage, moins il y a de fromage". La résolution de ce paradoxe peut se faire de pas mal de façons différentes, dont voici un exemple. Ici, on peut relever une contradiction : au début, on considère le vide des trous comme appartenant au fromage, alors que l'on considère le contraire au milieu du paradoxe (comme si nous ne parlions pas du même objet). Donc, la phrase "plus il y a de trous, moins il y a de fromages" est fausse, puis ce que les trous sont inclus dans ce que l'on appelle le fromage, la conclusion est donc aussi fausse. On peut tenter de ne parler que de la "partie consommable du fromage", mais la proposition devient beaucoup plus complexe, et (après étude) ne pose plus de paradoxe. De manière similaire, bien qu'une théorie puisse sembler fonctionnelle, il est parfois possible d'y trouver des incohérences. Cependant, il faut faire attention : certains objets mathématiques sont appelés paradoxe car ils donnent des résultats contre-intuitifs, en restant parfaitement justes. Ces cas précis seront listés au cas par cas.

Les différentes logiques possible

Maintenant que nous savons ce qu'est une proposition, et que nous savons déduire des propositions complexes de propositions plus simple, il ne nous reste plus qu'à savoir comment "déduire" des propositions, et donc comment utiliser des inférences. En effet, comme nous l'avons vu au chapitre 0 de ce cours, plusieurs écoles de philosophies des mathématiques existent pour "démontrer" un propos, et donc pour utiliser les inférences. Selon les auteurs (et leur "philosophie des mathématiques"), les inférences possibles entre plusieurs propriétés peuvent différer, et il est courant d'appeler les différents ensembles d'inférences possibles des "logiques différentes". Il est donc primordial de savoir avec quelle "logique" on va travailler dans la suite.

La logique des propositions / prédicats

La logique classique

Parmi toutes les "logiques" qui existent, une est assez intéressante pour comprendre comment les mathématiciens en sont arrivés là : la logique classique. Historiquement parlant, la logique classique est la première tentative de "parfaitement" formaliser la logique en mathématique au XIXème siècle. Cette logique apparaît au alentour des années 1880 grâce à un mec intelligent, et son livre "Begriffsschrift" ("L'idéographie" en français), bien que très vite rendu obsolète dans les années à venir. Dans les années 1890, le "prussien" (il est né en Prusse-Orientale) un mec intelligentpropose une logique améliorée, beaucoup plus proche de la logique actuelle.

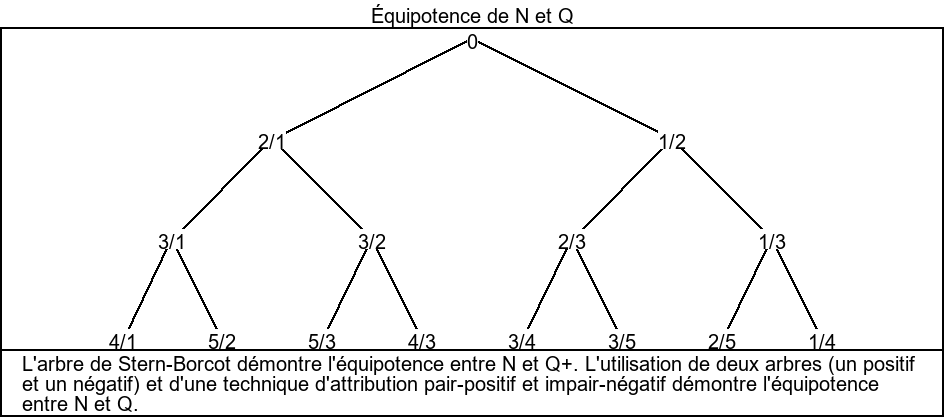
Historiquement, ce concept a frolé la catastrophe, à cause d'un évènement mathématique majeur : la crise des fondements. En effet, la crise des fondements est une période de l'histoire des mathématiques modernes, où la façon dont les mathématiques doivent fonctionner ont fortement été remises en question. Cette crise s'ammorce sur une question précise : et si les fondements utilisées en mathématiques étaient fausses, et que tout ce qui a été déduite via ces dernières l'étaient tout autant ? Cependant cela pose problème : dans les années 1830 (quand ces questions commencent), l'humanité était déjà relativement avancée en science, donc il ne devrait pas y avoir de problèmes. Or, de multiples résultats démontrèrent que des problèmes pouvaient toujours arriver (surtout en analyse). Plus tard, dans les années 1870, différents mathématiciens comme un mec intelligentdécouvrent des paradoxes étranges (Dedeking découvre qu'il y a "la même quantité" de nombres rationnels et de nombres naturels, mais pas de bijections entre les deux). Une grande partie des ces problèmes avait lieu à cause d'une définition... douteuse du concept d'infini. Or, les mathématiciens n'ont pas d'autres choix que de travailler avec, et continuent donc d'essayer de formaliser le plus précisément possible ces ensembles. Un des outils utilisés est la théorie des ensembles (que nous étudierons plus tard), résolvant pas mal de problèmes définitionnels, si utilisée sous forme de fondement des mathématiques. Or, au début des années 1900, cette théorie des ensembles se révèlent problèmatique, et de nombreux paradoxes y sont trouvé. De multiples corrections seront proposés pour résoudre ces problèmes. Au même moment, le concept de théorie mathématique s'affine, permettant de les étudier avec plus de précisions. Beaucoup de concepts apparaissent à ce moment là : cohérence, complétude, contradiction... Ces concepts mettrons un coup de grâce aux mathématiques, surtout à cause du mathématicien un mec intelligent. En effet, il publie un 1931 un théorème admettant que, dans le cas de la théorie des ensembles, nous ne pourrons jamais être sur que cette théorie ne soit pas incohérente. En d'autres termes, la théorie des ensembles (et donc presque toutes les mathématiques modernes) sont peut être complétement fausse, et nous ne savons pas encore pourquoi / comment. C'est ça, la crise des fondements. En réaction apparaissent les courants "philosophiques" des mathématiques, certains permettant d'éviter à coup sur les problèmes (mais à perte de beaucoup de théorèmes), tandis que d'autres continuent de s'appuyer sur la théorie des ensembles (mais à risque de tout perdre si elle se révèle fausse).

En logique classique, dans un contexte donné, une proposition est soit vrai soit fausse (jamais les deux). En d'autres termes, la valeur de vérité d'une proposition peut se représenter avec seulement 1 information (vrai ou faux). Cependant, si le contexte change, la valeur de vérité de la proposition peut changer. Bien que le nombre de contexte est souvent incommensurable, la proposition est, dans chacun de ces contextes, soit vraie, soit fausse. Même si ce concept peut paraître assez évident en logique, dans des cas où une formule dépend d'autres formules, établir sa valeur de vérité en fonction de ses propositions constituantes peut-être un peu dur. Heureusement, comme, dans tous les cas, une proposition est soit vrai soit fausse, c'est aussi le cas pour n'importe quelle proposition, aussi complexe soit elle (et aussi pour ses composantes). Donc, pour une proposition quelconque composée de "n" propositions différentes, ces "n" propositions peuvent toutes être soit vrai, soit fausse, et selon leurs valeur de vérité, la proposition composée est, elle aussi, soit vrai, soit fausse. Or, il est possible de représenter intuitivement cela, grâce à ce que l'on appelle une table de vérité. Une table de vérité est un moyen de représenter les valeurs de vérités une proposition composée selon chaque valeur possibles de chacune de ses propositions composantes. Ce concept peut être très pratique pour illustrer (voir démontrer) comment une proposition complexe se comporte avec ses propositions composantes. Voici deux exemples : une où la proposition "C" est vraie si "A" et "B" le sont toutes les deux (et fausses sinon), et "F" est vrai si "A" est vraie seule ou si "B" est vraie seule (et pas les deux en même temps). Théoriquement, on peut définir des proposition avec encore plus de composantes, mais la table devient longue à écrire (nous le démontrerons plus tard, mais la table doit contenir "2 exposant n" lignes).

Travailler avec des propositions

Dans un certain sens, la "logique des propositions" est la version moderne de la "logique classique". En effet, la logique des propositions (aussi nommé "calcul des propositions") est une forme de logique étudiant les propositions et les relations entre les propositions. Cette forme de logique va nous permettre d'introduire une syntaxe très importante pour mieux comprendre la logique mathématique. Effectivement, la logique propositionnelle nous permet de lier / mettre en relation des propositions entre elles, pour faire des propositions plus complexes. Bien évidemment, elle introduit aussi la syntaxe nécessaire pour le faire.

Pour complexifier nos formules, nous allons les écrire avec des connecteurs logiques. Un connecteur logique est un moyen d'écrire une proposition complexe en coupant cette proposition en "sous-propositions", et d'analyser la proposition de départ en analysant ces sous-propositions. Je vais maintenant vous introduire aux deux connecteurs logiques les plus importants : "et" et "ou".

Je vais maintenant vous introduire aux deux connecteurs logiques les plus importants : "et" et "ou".

Le connecteur logique "et" permet de lier deux propositions en une proposition finale "P", qui n'est vrai QUE SI les deux propositions de bases ("proposition 1" ET "proposition 2") sont vraies (sinon, elle est fausse). Donnons un exemple : "je suis de nationalité française ET je suis majeur". Pour l'analyser, on peut découper cette proposition comme cela : "je suis de nationalité française" ET "je suis majeur". Dans ce cas, on peut analyser indépendamment ces deux propositions. Si les deux sont vraies, alors "je suis de nationalité française ET je suis majeur" l'est aussi. D'ailleurs, cette proposition représente la définition même d'être "citoyen français". Donc, "je suis citoyen français" est vrai si "je suis de nationalité française" ET "je suis majeur" le sont aussi. Cette exemple est assez simple, puisque la phrase de départ comporte le mot "et", cependant, il y a des cas où il faut une certaine analyse pour comprendre les propositions a tirer. D'ailleurs, une proposition qui s'écrit avec un "ET" est nommée une conjonction. Si une proposition "P" s'écrit "A et B" (avec A et B deux autres propositions quelconques), alors on peut écrire "P" sous cette forme, avec un symbôle "chapeau" (représentant le "et") :

P \Leftrightarrow A \land B

En pratique, personne ne va vous insulter si vous écrivez "ET" à la place de ce chapeau. Sa table de vérité est :

Le connecteur logique "ou" permet de lier deux propositions en une proposition finale "P", qui n'est vrai QUE SI l'une des deux propositions de bases ("proposition 1" OU "proposition 2") est vraie, ou si les deux sont vraies (sinon, elle est fausse). Donnons un exemple : "je suis employé OU je suis patron". Pour l'analyser, on peut découper cette proposition comme cela : "je suis employé" OU "je suis patron". Comme dans notre exemple pour le "et", on peut analyser indépendamment ces deux propositions. Si l'une des deux est vraie (ou les deux sont vraies, ce qui est possible si vous êtes un auto-entrepreneur), alors "je suis employé OU je suis patron" l'est aussi. D'ailleurs, cette proposition représente la définition même d'être un "travailleur". Donc, "je suis travailleur" est vrai si "je suis employé", OU si "je suis patron", ou si je suis les deux. Encore une fois, cette exemple est assez simple, puisque la phrase de départ comporte le mot "et", cependant, il y a des cas où il faut une certaine analyse pour comprendre les propositions a tirer. D'ailleurs, une proposition qui s'écrit avec un "OU" est nommée une disjonction. Si une proposition "P" s'écrit "A ou B" (avec A et B deux autres propositions quelconques), alors on peut écrire "P" sous cette forme, avec un symbôle "chapeau" inversé (représentant le "ou") :

P \Leftrightarrow A \lor B

En pratique, comme avec le "et", personne ne va vous insulter si vous écrivez "OU" à la place de ce chapeau. D'ailleurs, demanière assez évidente, si "A et B" est vraie, alors "A ou B" est vraie (cependant, l'inverse n'est pas vraie : si "A ou B" est vraie, "A et B" ne l'est pas forcément). Sa table de vérité est :

Le principe du tiers-exclus et la négation logique

En logique classique, le "principe du tiers-exclus" est une forme d'axiome. En effet, le principe du tiers-exclu est un principe logique qui stipule que une proposition NE PEUT QU'ÊTRE vraie ou fausse, mais pas les deux en même temps. Il s'agit d'une loi logique extrêment (particulièrement) évidente : si A est vraie, alors A n'est pas fausse (wow).

Pour bien utiliser ce concept, il faut introduire un nouvel outil de langage : la négation logique d'une proposition. La négation d'une proposition A représente une autre proposition qui est égale à "A est fausse", aussi notée "pas A" ou "non A". Selon la logique que nous avons déjà vu : "A ou pas A". La négation de la proposition "A" s'écrit avec un petit symbôle :

\neg A

Bien qu'elle ne soit pas très intéressante, on peut construire sa table de vérité :

Cependant, en observant cette table, on peut remarquer quelque chose d'intéressant : la table de vérité de "pas A" est la table de vérité de "A" où les V et les F ont été inversés. En fait, la négation d'une proposition quelconque a pour table de vérité la table de vérité de la proposition de départ où on inverse les V et les F (les parties vraies deviennent fausses, et les parties fausses deviennent vraies). Si on essaye de construire la table de vérité de "pas (pas P)", on remarque qu'elle est parfaitement similaire à celle de P : donc "pas (pas P)" est égal à "P". Démontrer une proposition en démontrant que sa négation est fausse (ou mène à une contradiction logique absurde) est une méthode de raisonnement nommée le raisonnement par l'absurde.

\neg (\neg A) \Leftrightarrow A

On peut donc chercher la négation du "ET" et du "OU" (démontrée juste ici) :

Avec quelques observations, on se rend compte que la négation de "A et B" est "(pas A et pas B) ou (A et pas B) ou (B et pas A)". La négation de "A ou B" est "pas (A et B)". Donc, si nous avons une proposition quelconque, on peut en déduire sa négation, et si nous démontrons la validité / fausseté de la négation, alors on obtient la fausseté / validité de la proposition de départ. Si la négation est plus simple à démontrer que la proposition de départ, alors cela peut être un bon moyen de gagner du temps.

L'implication et l'équivalence

Maintenant, je vais vous présenter deux autres connecteurs, qui, quand on les découvrent, peuvent paraître plus abstrait : l'implication et l'équivalence.

Le connecteur logique "implique" permet de lier deux propositions en une proposition finale "P", qui, si "A implique B" n'est vrai QUE SI la proposition A n'est vraie QUE QUAND la proposition B l'est aussi. À l'inverse des deux autres connecteurs, nous ne pouvons pas intervertir A et B. En général, en français, le connecteur logique "A implique B" se traduit par "si A alors B". Pour l'analyser, prenons un exemple très proche de l'exemple du "ET" : "si je suis citoyen français, je suis de nationalité française". Dans ce cas, on peut analyser indépendamment les propositions "je suis citoyen français" et "je suis de nationalité française". Bien évidemment, si vous êtes citoyen français, vous êtes de nationalité française : "je suis citoyen français" implique "je suis de nationalité française", et ceux dans tous les cas. Cependant, l'inverse ("je suis de nationalité française" implique "je suis citoyen français") est fausse : un mineur de nationalité française n'est pas un citoyen français. Dans le cas de propositions quelconques "A" et "B", si vous avez une proposition P "A implique B", alors la proposition "B implique A" (où l'on inverse le A et le B) est nommée la réciproque de P (comme nous l'avons expérimenté, elle n'a pas toujours la même valeur de vérité que P).

La table de vérité de l'implication est assez difficile à déduire. Essayons de la construire pour la proposition P stipulant "A implique B". Pour rappel, Le connecteur logique "implique" permet de lier deux propositions en une proposition finale "P", qui, si "A implique B" n'est vrai QUE SI la proposition A n'est vraie QUE QUAND la proposition B l'est aussi. Donc, si "A et B", alors P est vraie. Or, si "pas A et pas B", alors rien n'empêche P d'être vraie. Finalement, si "B et pas A" est vraie, c'est la même chose : rien n'empêche P d'être vraie. Cependant, si "A et pas B" est vraie, alors "A" est vraie quand "B" ne l'est pas : l'implication est fausse. D'ailleurs, la proposition "A et pas B" est la négation de l'implication.

L'implication se note avec une sorte de double flèche (ici, "A implique B") :

A \Rightarrow B

L'implication est au coeur d'une loi logique assez évidente, mais qui est une règle d'inférence primaire de la logique : le modus ponens. Le modus ponens est est une loi logique affirmant que si "A implique B" et "A" est vraie, alors "B" est vraie. Cependant, ce n'est pas la seule loi d'inférence commenceant par "modus" : on dénombre aussi le modus tollens. le modus ponens est est une loi logique affirmant que si "A implique B" et "A" est vraie, alors "B" est vraie. Historiquement parlant, ces lois font parties d'un ensemble de lois similaires, développés par les grecques dans leur étude de la logique.

Il existe un moyen de démontrer plus facilement une implication : la contraposée. La contraposée est un moyen de prouver une implication P "A implique B", en prouvant que "pas A implique pas B". En d'autres termes : si A est fausse, alors B est aussi fausse. Ce raisonnement peut être plus simple dans certains cas.

Nous avons vu l'implication dans le cas où nous ne connaissons pas le comportement de sa réciproque. Cependant, si une implication et sa réciproque sont vraies, nous avons un nouveau type de connecteur : l'équivalence. Le connecteur logique "équivaut" permet de lier deux propositions en une proposition finale "P", qui n'est vraie QUE SI les deux propositions de bases sont toutes les deux vraies ou toutes les deux fausses (elles ont l'exact même valeur de vérité). Dans ce cas, sa table de vérité est exactement la même que celle de "(A implique B) ET (B implique A)". Réciproquement, d'une équivalence, on peut en déduire ces deux implications comme vraies. On peut en déduire que, dans une équivalence, l'ordre ne change pas ("A équivaut à B" est parfaitement... équivalent à "B équivaut à A"). D'ailleurs, démontrer "A équivaut à B" revient souvent à démontrer que "(A implique B) et (B implique A)". Un exemple assez simple est encore l'exemple du "ET" : comme nous l'avons prouvé, la proposition "être de nationalité française ET être majeur" est équivalente à la proposition "être citoyen français" (sauf si les institutions ne font pas leur travail, mais cela reste rare). Une propriété très intéressante : si deux propriétés sont équivalentes, alors remplacer l'une d'elle par l'autre ne change absolument pas les valeurs de vérités, et donc ne pose aucun problème logique.

L'équivalence se note comme l'implication, avec une flèches sur les deux bords :

A \Leftrightarrow B

Travailler avec les prédicats

Pour l'instant, nous nous sommes mis d'accord sur le fait que toute proposition est soit vraie, soit fausse, et pas les deux. Cependant, imaginez une proposition "le nombre n est pair". Sa véracité dpend entièrement du nombre "n", qui est une variable : elle peut donc être vraie ou fausse selon n, ce qui, au mieux, rentre en contradiction avec la définition de proposition, et au pire pose de gros problèmes de logique. Heureusement, pour travailler avec des variables dans des propositions, on peut utiliser un autre objet : un prédicat. Un prédicat est un schéma de proposition utilisant une variable externe, qui permet d'obtenir une proposition concrète (soit vraie soit fausse) selon la valeur précise de la variable. Dans ce cas, "le nombre n est pair" est un prédicat, qui est vrai si... n est pair (2, 4, 6...).

Cependant, il est possible de transformer un prédicat en une proposition, de manière assez simple. En effet, reprenons notre prédicat d'exemple : "le nombre n est pair". Vu comme ça, nous ne pouvons pas en tirer grand chose. Cependant, il existe un objet mathématique qui va nous permettre d'en obtenir une proposition : les quantificateurs. En logique mathématique, un quantificateur est un objet mathématique utilisable pour poser le contexte d'utilisation de la variable d'un prédicat (la transformant en proposition). En fait, avec un quantificateur, on transforme le prédicat en une proposition, en changeant la façon dont le prédicat doit interpréter la variable (de telle manière que le prédicat devient une proposition). D'un point de vu purement vocabulaire, la quantification (en logique mathématique) est l'action de quantifier un prédicat quelconque. Pour bien comprendre, il nous faut voir les deux quantificateurs principaux : le quantificateur universel et le quantificateur existentiel.

Le premier quantificateur utilisé est le quantificateur universel. Le quantificateur universel transforme un prédicat en une proposition vraie si TOUTES les propositions formulables avec ce prédicat sont vraie. En d'autres termes, si la proposition constitué d'un quantificateur universel d'une variable et un prédicat est vraie, alors toutes les propositions de ce prédicat seront vraie, quelle qu'elle soit. Généralement, pour une variable "x", ce quantificateur se traduit à l'écrit sous la forme "pour tout x", "tous les x"... Dans notre exemple, on peut formuler la proposition sous cette forme : "tous les nombres n sont pairs", une proposition qui est fausse. En effet, il existe des nombres entiers "n" qui ne sont pas pair (comme 3). Cependant, la proposition "tous les nombres n admettent un élément supérieur, noté n + 1" est vraie (testez avec tous les nombres "n" que vous voulez, il y aura toujours un nombre "n + 1"). Pour un prédicat "P(n)", la proposition "pour tout n, P(n)" s'écrit comme ça (avec un "A" verticalement inversé, représentant le quantificateur universel, venant du mot allemand "alle", voulant dire "tous") :

\forall n, P(n)

Ici, il manque juste la mention de "nombres", que nous introduirons plus tard. Sans cette mention, il est admis que la nature du "n" dépend du contexte de la formule.

Le deuxième quantificateur utilisé est le quantificateur existentiel. Le quantificateur existentiel transforme un prédicat en une proposition vraie si il existe AU MOINS UNE proposition vraie formulable avec ce prédicat. En d'autres termes, si la proposition constitué d'un quantificateur existentiel d'une variable et un prédicat est vraie, alors il existe une (ou plusieurs) proposition de ce prédicat vraie. Généralement, pour une variable "x", ce quantificateur se traduit à l'écrit sous la forme "il existe un x tel que". Dans notre exemple, on peut formuler la proposition sous cette forme : "il existe un nombre n pair", une proposition qui est vraie. En effet, il existe au moins un (et même, une infinité) nombre entier "n" qui est pair : 2. Cependant, la proposition "il existe un nombre n admettant une partie décimale non nulle" est fausse (de manière assez évident, aucun nombre entier ne s'écrit avec des nombres après la virgule). Pour un prédicat "P(n)", la proposition "il existe un n tel que P(n)" s'écrit comme ça (avec un "E" horizontalement inversé, représentant le quantificateur existentiel) :

\exists n, P(n)

Même problème que pour le quantificateur universel : il manque la mention de "nombres", que nous introduirons aussi plus tard. Comme pour avant, sans cette mention, il est admis que la nature du "n" dépend du contexte de la formule.

Comme nous l'avons évoqué, il est possible de formuler la négation de propositions construites avec un quantificateur. Dans le cas du quantificateur universel, une proposition utilisant le quantificateur universel pour une variable "n" est fausse si il existe un (ou plusieurs) "n" quelconque donnant une proposition fausse. Donc :

\neg (\forall n, P(n)) \Leftrightarrow (\exists n, \neg P(n))

Dans le cas du quantificateur existentiel, une proposition utilisant le quantificateur existentiel pour une variable "n" est fausse si TOUS les "n" donnent une proposition fausse. Donc :

\neg (\exists n, P(n)) \Leftrightarrow (\forall n, \neg P(n))

La théorie des ensembles

La théorie centrale des mathématiques

La théorie des ensembles

Maintenant que nous avons les bases de la logique, nous pouvons aborder notre première théorie mathématique importante : la théorie des ensembles. La théorie des ensembles est une théorie mathématique développé à la fin du XIXème siècle, pour être utilisée comme socle des mathématiques. Son principal fondateur est le mathématicien allemand un mec intelligent, qui l'a proposé dans une suite d'articles mathématiques entre 1874 et 1900. L'idée semblait être complexe : unir toutes les mathématiques (nombres, géométries, fonctions...) sous une seule théorie. Même si, historiquement, cette théorie a mis beaucoup de temps à se faire accepter, elle a finalement réussi sa mission : presque toutes les mathématiques modernes en dépend.

Ici, un ensemble est un objet mathématique qui peut "contenir" d'autres objets (on dit que ces objets appartiennent à l'ensemble), et qui est parfaitement cohérent dans la théorie des ensembles. Cette définition se rapproche beaucoup d'une autre : celle des classes. Une classe est un objet mathématique qui peut "contenir" d'autres objets (on dit que ces objets appartiennent à l'ensemble), mais qui n'est pas forcément cohérent dans la théorie des ensembles. Ceci peut paraître assez bizarre, mais une classe peut ne pas fonctionner dans la théorie que nous allons énoncer (là où un ensemble doit obligatoire fonctionner), comme elle peut fonctionner (dans ce cas, elle est aussi un ensemble). D'ailleurs, un ensemble est une classe, mais une classe n'est pas forcément un ensemble. Nous verrons plus tard en quoi cette distinction est utile. Une façon intéressante de représenter un ensemble peut être la suivante (ici, l'ensemble des nombres impairs entre 0 et 10) :

Il existe un symbôle précis pour indiquer qu'on objet "a" appartient à un ensemble "S" :

a \in S

D'ailleurs, "l'objet "a" appartient à l'ensemble "S"" est une proposition, dont la véricaté dépend de... beaucoup de choses (généralement dépendant du contexte précis de "a" ou "S"). Ce symbôle permet de faire quelque chose de très intéressant : on peut utiliser ce symbôle dans un quantificateur logique, pour spécifier qu'on objet que l'on quantifie appartient à un certain ensemble. Nous pouvons donc répondre à la question de tout à l'heure "comment spécifier que notre proposition "pour tout n, P(n)" ne fonctionne qu'avec des nombres" : on a juste à rajouter ce symbôle (on admet pour l'instant que "N" est l'ensemble des nombres entiers naturels) :

\exists n \in N, P(n)

Puisque l'on parle d'ensembles, parlons d'un terme extrêment similaire : un sous-ensemble. Un sous-ensemble (ou partie) d'un ensemble A est un ensemble contenant uniquement des éléments de A (et pas plus). Il n'est pas exclu qu'un sous-ensemble contienne la totalité des éléments de A... comme ne contient aucun élément (il est défini comme étant quand même un sous-ensemble de A). Ce concept nous permet d'en introduire un autre : l'inclusion. Un ensemble est dit inclu dans un autre ensemble B lorsque que TOUS ses éléments appartiennent aussi à B. Donc, si un ensemble A est inclu dans un autre ensemble B, alors A est un sous-ensemble de B (et vice-versa, si A est un sous-ensemble de B, alors il est inclu dans B). La notation mathématique est assez similaire à celle de l'appartenance, à la différence prêt que le "U" retourné n'est pas barré. Vous trouverez aussi la définition mathématique rigoureuse du concept. Pour une traduction mathématique - français, lisez "pour tout ensemble A et B, A est inclu ou égal à B si (et seulement si) pour tous les éléments possibles, si un élément appartient à A, alors il appartient à B".

\forall A \forall B, A \subseteq B \Leftrightarrow \forall x (x \in A \Rightarrow x \in B)

Cette notation autorise A à être égal à B : on pourrait parler de "inclu ou égal". Cependant, il existe une notation où A n'est pas égal à B, nommée "inclusion stricte", se notant avec une petite barre en dessous du "U", toujours avec la définition mathématique rigoureuse. Pour une traduction mathématique - français, lisez "pour tout ensemble A et B, A est strictement inclu dans B si (et seulement si) pour tous les éléments possibles, si un élément appartient à A, alors il appartient à B, et si il existe un élément dans B qui n'est pas dans A".

\forall A \forall B, A \subset B \Leftrightarrow [\forall x (x \in A \Rightarrow x \in B) \land \exists y \in B (y \notin A)]

La théorie des ensembles "ZFC"

La première version de la théorie proposée par Cantor n'était pas très bien axiomatisée. Une version plus solide apparaîtra entre les années 1908 et 1920 : la théorie des ensembles "ZFC". La théorie des ensemble "ZFC" (pour Zemerlo - Fraenkel - choix) est une version axiomatisée et cohérente (pour l'instant) de la théorie des ensembles de Cantor. Comme son nom l'indique, elle a été développée par 2 mathématiciens majoritairement : un mec intelligentet un mec intelligent. Le suffixe "choix" représente un axiome précis, que l'on peut ignorer (dans ce cas, on parle de théorie des ensembles "ZF"). Présentons les premiers axiomes de cette théorie, proposés par Zemerlo entre 1889 et 1908.

Le premier axiome est l'axiome d'extensionnalité. L'axiome d'extensionnalité dit que si deux ensembles possèdent exactement les mêmes éléments, alors ils sont égaux. Dans le cas d'ensembles normaux, l'ordre des éléments n'importe pas. De manière illustré, l'axiome confirme cette égalité :

Cet axiome permet d'introduire une première manière de définir un ensemble : la définition par extension. Un ensemble est dit "défini par extension" quand il est défini par une égalité avec un ensemble dont les éléments sont explicitement indiqués. Ce nom vient du fait que c'est l'axiome d'extension qui permet d'attribuer les éléments voulus à l'ensemble. Voici quelques exemples de définitions par extension :

A = {1, 10, 100, 1000}

A = {72}

A = {0, 1, 2, 3, 4, 5, 6, 7, 8}

Il est à noter que, en général, ces ensembles sont notés entre crochets "{}", avec des éléments séparés par des virgules, ou des points virgules. De manière purement mathématique, l'axiome peut s'énoncer de plusieurs manières équivalentes. La première n'utilise que des équivalences, et la deuxième découpe la première équivalence en deux implications (généralement plus utilisé dans les démonstrations). Pour une traduction mathématique - français, lisez "pour tout ensemble A et B, A et B sont égaux si (et seulement si) tous les éléments de B sont des éléments de A, et tous les éléments de A sont des éléments de B".

\forall A \forall B [\forall x (x \in A \Leftrightarrow x \in B) \Leftrightarrow A = B]

\forall A \forall B [(\forall x {x \in A \Rightarrow x \in B} ET \forall x {x \in B \Rightarrow x \in A}) \Leftrightarrow A = B]

Pour prouver simplement que deux ensembles sont les mêmes, il existe une technique assez puissante : la double inclusion. Deux ensembles A et B sont égaux si (et seulement si) A est "inclu ou égal" à B et B est "inclu ou égal" à A. Cette proposition se démontre assez facilement grâce à cette axiome.

\forall A \forall B (A \subseteq B \land B \subseteq A \Leftrightarrow A = B)

Le deuxième axiome est l'axiome de l'ensemble vide. L'axiome de l'ensemble vide est un axiome garantissant l'existence d'un ensemble vide dans la théorie. Comme son nom l'indique : l'ensemble vide est un ensemble ne contenant aucun élément. Par définition, la proposition "l'élément "e" appartient à l'ensemble vide" est toujours fausse. Selon l'axiome d'extensionnalité, on en déduit qu'il n'y en a qu'un seul (démontré ici). En réalité, certains auteurs négligent cet axiome, car il peut être déduit grâce à des théorèmes beaucoup (mais alors, vraiment beaucoup) plus complexes. Cet ensemble se note ainsi :

\emptyset

De manière purement mathématique, cet axiome est assez simple à énoncer. Pour une traduction mathématique - français, lisez "il existe un ensemble noté [symbôle de l'ensemble vide] tel que, pour tout "x", "x" n'appartient pas à [symbôle de l'ensemble vide]".

\exists \emptyset \forall x, \neg [x \in \emptyset]

Le troisième axiome est l'axiome de la paire. L'axiome de la paire est un axiome confirmant que, pour deux ensembles quelconques A et B, il existe un ensemble contenant deux éléments : A et B (nommée paire de A et B). Cet axiome peut paraître assez évident, mais il reste important à énumérer. Selon l'axiome d'extensionnalité, on en déduit qu'il n'y en a qu'un seul (démontré ici).

De manière purement mathématique, cet axiome est aussi assez simple à énoncer, mais un peu plus dur à traduire. Pour une traduction mathématique - français, lisez "pour tout ensemble A et B, il existe un ensemble C dont les éléments sont TOUS les éléments possibles qui sont soit A, soit B".

\forall A \forall B \exists C \forall x [x \in C \Leftrightarrow (x = A \lor x = B)]

Le quatrième axiome est l'axiome de la réunion. L'axiome de la réunion affirme que, pour tout ensemble A dont les éléments sont des ensembles, il existe un ensemble B tel que tous ces éléments appartiennent à un sous-ensemble C de A, et tous les éléments des sous-ensembles de A appartiennt à B. Cet axiome peut paraître un peu bizarre, mais il est cependant très important dans plein de démonstrations. Par exemple, en le couplant avec l'axiome de la paire, on peut prouver qu'il existe un ensemble C tel que, pour tout ensemble A et B, C est composé de tous les éléments de A et B (et pas plus).

De manière purement mathématique, cet axiome est assez difficile à énoncer... et aussi à traduire. Pour une traduction mathématique - français, lisez "pour tout ensemble A, il existe un ensemble B dont les éléments sont TOUS les éléments possibles tel qu'il existe un ensemble C dans A tel que B appartiennent à C".

\forall A \exists B \forall x [x \in B \Leftrightarrow \exists C (C \in A \land x \in C)]

Le cinquième axiome est l'axiome de l'ensemble des parties. L'axiome de l'ensemble des parties est un axiome qui assure l'existence, pour tout ensemble A, d'un ensemble des parties de A. En théorie des ensembles, l'ensemble des parties (ou ensemble puissance) d'un ensemble E est un ensemble contenant la totalité des sous-ensembles (pas forcément ordonnés) possibles dans l'ensemble E (en incluant l'ensemble vide et E). Comme pour les autres axiomes, il peut paraître relativement évident, mais reste assez important dans la théorie. Il ne faut cependant pas oublier de lui ajouter certains sous-ensembles de A souvent oubliés : A lui même et l'ensemble vide.

De manière purement mathématique, cet axiome est assez facile à énoncer et à traduire. Pour une traduction mathématique - français, lisez "pour tout ensemble A, il existe un ensemble P dont les éléments sont TOUS les éléments possibles inclus dans A".

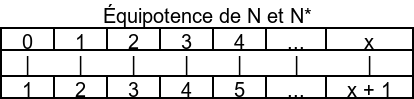
\forall A \exists P \forall B (B \in P \Leftrightarrow B \subseteq A)

Le sixième axiome est l'axiome de l'infini. Cet axiome est un peu bizarre, mais infiniment important (sans mauvais jeu de mots). L'axiome de l'infini stipule qu'il existe un ensemble contenant un élément de départ nommé "0", et tel que tous les éléments "n" de cet ensemble admettent un élément précis (défini via une fonction), nommé "successeur de n" ou "successeur(n)". Les premiers éléments de cet ensemble sont "0", "successeur(0)", "successeur(successeur(0))"... En fait, cet ensemble représente exactement l'ensemble des nombres entiers naturels, noté "N"(qui respectent eux aussi cette exacte propriété). Dans ce cas, on peut écrire "successeur(n)" comme "n + 1" (on défini donc l'opération "a + b" comme l'utilisation de la fonction successeur "b" fois sur un nombre entier naturel "a"). Nous définirons toutes les propriétés nécessaires dans la dernière partie du chapitre. Comme pour tout nombre naturel, on peut trouver un nombre supérieur (sous la forme "n + 1"), cette ensemble admet une infinité d'éléments (d'où le nom de l'axiome).

De manière purement mathématique, cet axiome est... difficile à énoncer. En réalité, il est théoriquement possible de l'énoncer de plusieurs façons différentes. Dans notre cas, nous allons utiliser la version proposée par le mathématicien hongrois un mec intelligent. Ce mathématicien a proposé une façon assez pratique de solidement construire cette ensemble : le "0" représente l'ensemble vide, et le "successeur" comme une fonction transformant un élément "b" en un ensemble représentant l'union de l'ensemble ne contenant que "b" et de "b" lui même. Pour une traduction mathématique - français, lisez "il existe un ensemble A qui contient l'ensemble vide et dont tout élément "b" admet un "successeur" (appartenant à A) si il appartient à A".

\exists A [\emptyset \in A \land \forall b (b \in A \Rightarrow b \cup {b} \in A)]

Cette axiome nous permet de faire quelque chose de très intéressant : introduire une nouvelle forme de raisonnement. En effet, il nous permet d'introduire le raisonnement dit "par récurrence". Le raisonnement par récurrence est un principe de raisonnement permettant de prouver que si un prédicat "P(n)" est vraie pour "P(a)" et que, pour tout élément "k" d'un ensemble "N", "P(k) implique p(successeur(k))", alors "P(n)" est vraie pour tout "n" supérieur à "a". En utilisant le formalisme des nombres, on peut dire que, si "P(0)" est vraie et "P(n) implique P(n + 1)", alors "P(1)" est vraie, "P(2)" aussi, et tout "P(n)" l'est également. Ce type de raisonnement nous sera très utile dans pleins de contextes impliquant cette axiome (et donc, impliquant les nombres entiers naturels).

Le septième axiome n'est... pas un axiome à proprement parlé, mais un schéma d'axiome : le schéma d'axiome de compréhension. Le schéma d'axiome de compréhension est un schéma d'axiome construisant un axiome par propriété, stipulant que, pour tout ensemble "A", il existe une classe "B" dont tous les éléments sont les éléments de A rendant une propriété "P" vraie (déduite grâce aux autres axiomes). Ici, on défini bien "B" comme une classe, car il peut poser certains problèmes dans ZFC (que nous verrons juste après ce schéma d'axiome). Cependant, un axiome que nous définirons tout à l'heure nous permet d'affirmer que "B" est presque toujours un ensemble(ce qui est possible car un ensemble est une classe). Si aucun élément de l'ensemble ne vérifie la propriété, alors l'ensemble obtenu est l'ensemble vide. Cet axiome permet de faire quelque chose de très pratique : introduire la définition d'ensemble par compréhension. Un ensemble est dit "défini en compréhension" quand il est défini comme tous les éléments d'un autre ensemble vérifiant une propriété spécifique. Ce nom vient du fait que c'est le schéma d'axiome de compréhension qui atteste de l'existence de cette ensemble. De manière abstraite, un ensemble B défini par compréhension s'énonce comme ceci (lisez "B est l'ensemble de tous les éléments x possibles respectant la propriété P(x) (et donc, où P(x) est vraie)") :

B = {x, P(x)}

Prenons un exemple plus concret : un ensemble A défini par extension et un ensemble B défini par compréhension. Pour définir l'axiome B comme tous les éléments de A vérifiant la propriété P "l'élément est pair", on doit utiliser une relation d'appartenance entre "x" et "A" :

A = {1, 2, 3, 4, 5, 6, 7, 8}

B = {x \in A, P(x)} = {2, 4, 6, 8}

De manière purement mathématique, cet axiome est moyennement complexe à énoncer et à traduire. Nous allons commencer par citer une version simplifiée, puis la version finale. Pour une traduction mathématique - français de la version simplifiée (la première), lisez "pour tout ensemble A, il existe un ensemble B tel que, pour tout élément "x" de B, "x" est un élément de A et "x" respecte la propriété "P"". Pour une traduction mathématique - français de la version complète (la seconde, où l'on introduit le fait que la propriété puisse avoir besoin de variables indépendantes), lisez "pour toute variable "v0", "v1" ... jusq'à "vn", pour tout ensemble A, il existe un ensemble B tel que, pour tout élément "x" de B, "x" est un élément de A et "x" respecte la propriété "P" à laquelle on applique les variables du début de l'axiome".

\forall A \exists B \forall x [x \in B \Leftrightarrow (x \in A \land P(x))]

\forall v_{0} ... \forall v_{n} \forall A \exists B \forall x [x \in B \Leftrightarrow (x \in A \land P(x, v0, ..., vn))]

Sur cet axiome s'achève notre présentation des axiomes proposés par Zemerlo en première instance. Cependant, cette théorie est insuffisante, et admet une quantité monstrueuse de paradoxes (paradoxes de Russell, paradoxe de Richard, paradoxe de Berry...). Historiquement, le plus connue est celui de Russell. En effet, le paradoxe de Russell est un paradoxe de la théorie des ensembles proposé par Zemerlo, où Russell crée un ensemble représentant l'ensemble des ensembles n'appartenant pas à eux-mêmes (autorisé par le schéma axiome de compréhension), mais qui ne peut ni appartenir ni ne pas appartenir à lui même (ce qui pose une contradiction). Donc, cet ensemble ne peut pas exister : le schéma d'axiome de compréhension est donc incohérent. Déjà, il faut savoir que, lors de la publication originale de la théorie des ensembles, des axiomes similaires à "l'axiome de compréhension" existés déjà, et presque tous admettaient que "B" est un ensemble. Ce paradoxe démontre que, si l'axiome de compréhension permet de toujours admettre que "B" est un ensemble, alors des paradoxes logiques apparaissent.

Une version corrigée était nécessaire : c'est ce que va fraire Fraenkel. En 1922, Fraenkel publie en 1922 une version complétée de la théorie, nommée "théorie des ensembles ZF", où beaucoup de ces paradoxes sont résolues. Cette théorie modifie légèrement les axiomes que nous avons déjà vu, et rajoute un nouvel axiome et un nouveau schéma d'axiome. C'est dans ce contexte là que "B" a dû être assumé comme étant une classe, qui est très souvent (dans les mathématiques courantes) un ensemble.

L'axiome proposé par Fraenkel est l'axiome de fondation. L'axiome de fondation est un axiome obligeant tout ensemble "A" à posséder un élément qui, dans sa forme "ensemble", ne contient aucun élément de "A". Ici, quand on dit qu'un élément est sous une forme "ensemble", cela signifie que nous devons l'utiliser comme un ensemble (ce qui est, dans ZFC, toujours possible, quelque soit l'élément : nombre, espaces... mais nous verrons comment plus tard). Cet axiome peut aussi sembler un peu bizarre, mais il permet de contrer quelques-uns des paradoxes de la théorie. En effet, en l'utilisant avec l'axiome de l'ensemble des parties, on peut démontrer un résultat très important : un ensemble ne peut pas se contenir lui même, et aucun élément (sous forme d'ensemble) d'un ensemble contient ce même ensemble (ni les éléments des éléments...), démontré juste ici.

Cette axiome n'est pas très dur à énoncer, mais un peu plus à traduire. Pour une traduction mathématique - français, lisez "pour tout ensemble x, si x n'est pas vide, alors il existe un élément de y qui, dans sa forme (ensemble), ne contient aucun élément de x".

\forall x [x \neq \emptyset \Rightarrow \exists y (y \in x \land y \cap x = \emptyset)]

Finalement, le dernier schéma d'axiome obligatoire proposé par Fraenkel est le schéma d'axiome de remplacement. Le schéma d'axiome de remplacement est un schéma d'axiome garantissant que toute classe se comportant comme une fonction peut être restreinte à un ensemble se comportant comme une fonction (en utilisant comme antécédent un ensemble). À l'inverse des autres axiomes, celui si n'est ni simple, ni intuitif, et nous y reviendrons quand nous parlerons de la logique mathématique avancée. Cependant, il permet de résoudre beaucoup de paradoxes que nous avons vu auparavant. En effet, c'est ce schéma d'axiome qui stipule si une classe obtenue via l'axiome de compréhension est une classe ou un ensemble.

L'axiome du choix

L'axiome du choix est un axiome assez bizarre, car il n'est pas aussi utilisé que les autresn et parfois exclu de la théorie. L'axiome du choix est un axiome permettant l'existence d'un moyen d'extraire un élément quelconque d'un ensemble, une infinité de fois (et donc, dans une infinité d'ensemble), pour construire un nouvel ensemble. Pour des raisons de formalisme, l'axiome dit que tous ces ensembles doivent être défini dans un ensemble plus grand (bien que ça ne change rien au coeur du concept). Nuance importante : l'axiome permet l'existence de ce moyen, mais il n'oblige pas à l'expliciter. En général, ce moyen est une fonction (si vous ne savez pas ce que c'est, ou que vous ne savez pas bien le définir, voyez cela comme le nom que l'on donne à ce moyen). Donc, ce moyen peut être parfaitement naturel, comme totalement aléatoire (et non-explicité).

L'idée de cet axiome est de pouvoir utiliser cette fameuse "fonction", dans des cas divers et variés, et dans des ensembles infinis. Son énoncé mathématique est... assez complexe. Pour une traduction mathématique - français, lisez "pour tout ensemble X non vide, il existe une fonction f allant de X vers la réunion de tous les ensembles A appartenant à X (comme permis par l'axiome de la réunion), transformant les éléments A de X (des ensembles) en un élément quelconque de A".

\forall X[X \neq \emptyset \Rightarrow \exists f:X ⟶ \cup X \forall A \in X(f(A) \in A)]

Les propriétés basiques des ensembles

Les ensembles peuvent posséder un grand nombre de propriétés, souvent assez basiques.

La propriété la plus "évidente" d'un ensemble est son cardinal. Le cardinal d'un ensemble est une façon de représenter le nombre d'éléments que contient l'ensemble. Cette définition est infiniment plus simple dans le cas où l'ensemble est fini. Ici, un ensemble est "fini" si il n'est pas possible de trouver de nouveaux éléments dans l'ensemble (que nous n'avons pas déjà trouvé) après en avoir consulter une certaine quantité. Le cardinal d'un ensemble fini est un nombre (entier naturel) représentant le nombre d'éléments distincts appartenant à l'ensemble. Par exemple, le cardinal de l'ensemble {1, 3, 4, 7, 9} est 5 (il y a 5 éléments dedans). La définition rigoureuse (avec des symbôles mathématiques complexes et tout le bazard) est particulièrement complexe, et nous ne pouvons pas l'étudier pour l'instant (dans le cas des ensembles finis, nous nous contenterons de compter les éléments dans l'ensemble).

Singletons, pairs et couples

Nous allons présenté quelques mots de vocabulaire assez simple, mais très utilisé. Un singleton est ensemble fini de cardinal 1 (il ne contient qu'un seul élément). En général, ces ensembles sont presque toujours exprimé en extension (comme le singletion {5}). On peut assez facilement prouver que, pour tout élément possible, il existe (obligatoirement) un singleton contenant cet élément : utilisez l'axiome de la paire sur cet élément et l'ensemble vide, puis l'axiome de la réunion sur l'ensemble obtenu, et vous obtenez le singleton voulu. Un concept assez similaire est la paire. Une paire est ensemble fini de cardinal 2 (il ne contient que deux éléments). Dans la théorie ZFC, son existence est garantie par l'axiome de la paire, présenté plus haut.

Comme nous l'avons vu, dans un ensemble, l'ordre n'importe pas, voir n'existe pas : c'est donc le cas pour la paire. Cependant, il est possible de donner un ordre aux éléments d'une paire, grâce à un autre objet similaire : le couple. Un couple est une paire où un des deux objets doit être écrit avant l'autre (et donc, il s'agit d'une paire où il y a un ordre d'écriture des éléments). Il s'agit toujours d'un ensemble, mais défini de manière un peu différente, pour donner un ordre aux éléments. Jetons un petit coup d'oeil à ce qui différencie une paire d'un couple dans leur définition. Une paire peut simplement être écrit comme ça :

A = {1, 2} = {2, 1}

Ici, l'ordre n'a pas d'importance. Donc, nous allons devoir trouver un moyen permettant d'écrire des couples, pour rendre l'ordre important. Déjà, notons que l'écriture d'un couple se fait en remplaçant les accolades par des parenthèses. Nous allons utiliser la représentation proposé par le mathématicien polonais un mec intelligent. Dans cette proposition, un couple "C" formé d'un élément "x" puis d'un élément "y" se note :

C = (x, y) = {{x}, {x, y}} = {{x, y}, {x}}

Dans ce cas, le couple devient un ensemble contenant deux éléments : un singleton contenant le premier élément, et une paire contenant les deux éléments. On peut donc distinguer le premier élément de l'autre. On peut écrire le couple opposé, est constater (grâce à l'axiome d'extension) qu'il n'est pas égal au couple de départ (le singleton du "premier élément" n'est pas le même) :

C = (y, x) = {{y}, {x, y}} = {{x, y}, {y}} \neq (x, y) = {{x, y}, {x}}

L'obtension du premier élément se fait donc par le singleton, et l'obtension du second se fait en prenant l'élément de la paire qui n'est pas dans le singleton.

Les opérations sur les ensembles

L'union et l'intersection

L'union et l'intersection sont des opérateurs permettant de réaliser une opération logique entre deux ensembles. En effet, l'union (ou réunion) de deux ensembles A et B représente un nouvel ensemble C qui contient tous les éléments de A et de B (tous les éléments qui sont dans A ou dans B). En terme mathématique (lisez "pour tout ensemble A et B, il existe un ensemble C tel que, pour tous les éléments x possibles, x est dans C équivaut à dire que x est dans A ou B (ou les deux)") :

\forall A \forall B, \exists C \forall x {x \in C \Leftrightarrow x \in A \lor x \in B}

Les deux appellations (union et réunion) sont possibles, et désignent l'exact même chose. Son existence est assez facilement déductible, grâce à la combinaison de l'axiome de la paire et de l'axiome de la réunion. En fait, "l'union" est un opérateur, ce marquant avec une sorte de grand "U" :

A \cup B = C

C'est assez simple à illustrer.

L'intersection est un opérateur aussi simple à comprendre. L'intersection de deux ensembles A et B représente un nouvel ensemble C qui contient tous les éléments étant en même temps dans A et dans B. Il s'agit de l'union où vous remplacez le "ou" de la définition mathématique par un "et". En terme mathématique (lisez "pour tout ensemble A et B, il existe un ensemble C tel que, pour tous les éléments x possibles, x est dans C équivaut à dire que x est dans A et B") :

\forall A \forall B, \exists C \forall x {x \in C \Leftrightarrow x \in A \land x \in B}

Si les deux ensembles ne partagent aucun élément en commun, C vaudra l'ensemble vide. Dans ce cas, ces deux ensembles sont dits "disjoints". Son existence demande un peu plus de réflexion, mais se déduit grâce à l'axiome de l'ensemble vide. Cet opérateur se marque avec le même symbôle que l'union à l'envers :

A \cap B = C

Il est aussi assez simple à illustrer.

Grâce à ces deux concepts, vous pouvez en définir un autre assez pratique : les partitions d'un ensembles. Une partition d'un ensemble "E" représente un ensemble ne contenant que des parties non-vides de "E", toutes disjointes, et dont l'union de toutes ces parties donnent "E".

Le produit cartésien

Le produit cartésien est une opération très importante pour pas mal d'autres objets mathématiques. Le produit cartésien (aussi nommé produit cartésien binaire) de deux ensembles est une opération sur deux ensembles, permettant d'obtenir un ensemble contenant tous les couples possibles entre chaque élément du premier ensemble et chaque élément du second ensemble (dans cet ordre précis). Voici un exemple assez simple : le tableau qui suit représente le produit cartésien (cases blanches) de l'ensemble {1, 2, 3, 4, 5} (cases rouges) et de l'ensemble {1, 2, 3, 4, 5} (cases bleues).

Voici un autre exemple : le tableau qui suit représente le produit cartésien (cases blanches) de l'ensemble {A, B, C, D} (cases rouges) et de l'ensemble {1, 2, 3, 4, 5} (cases bleues).

La définition mathématique pure de cet opérateur est assez simple :

\forall E \forall F, \exists C, C = E X F \Leftrightarrow \forall x, y, {(x, y) \in C \Leftrightarrow x \in E \land y \in F}

Quelque soit les ensembles de départ, les utiliser via cet opérateur donne un nouvel ensemble fonctionnel (démontré ici), et heuresement, car il serait difficile de s'imaginer qu'il existe des ensembles pour lesquelles cela ne marche pas.

Les relations et applications mathématiques

Les objets centraux des mathématiques

Qu'est ce qu'est une relation mathématique ?

Avant d'introduire quoi que ce soit d'autre en mathématiques, un objet extrêmement important est l'application mathématique. En mathématique, une relation est un objet permettant d'énoncer des propositions entre plusieurs éléments d'un même ensemble quelconque. Par exemple, dans un ensemble de nombres entiers naturels, la relation "inférieur" est définie, et donne une proposition juste juste pour tout "m" et "n" où... m est inférieur à n (comme "3 est inférieur à 5"). Cette définition pose un problème : il existe des objets infiniment proche de cette définition, mais qui n'en font pas partie, car pas "dans un même ensemble quelconque". C'est le cas de la relation d'appartenance "un élément a appartient à un ensemble E", où il n'existe pas vraiment "d'ensemble" généralisant en même temps le concept d'élément et d'ensemble. Pour éviter ce problème, nous allons dire que, dans ce cas précis, on ne parle pas d'ensemble, mais de classe (il existe une classe contenant tous les ensembles et éléments possibles). Pour tout le reste, la définition avec les ensembles fonctionne. Il est très fréquent (voir même, presque tout le temps appliqué) d'appeler une relation avec un simple symbôle comme "=", "<" ou "~", et de disposer les objets à lier entre eux aux côtés de la relation, comme "3 + 4 = 7". Deux éléments "a" et "b" liés par une relation "~" sont dit "en relation entre eux par la relation "~"".

Le concept de relation est donc un moyen "syntaxique" d'énoncer des proprositions facilement. Comme tout objet "syntaxique", la chose la plus importante avec ces relations est la façon dont on l'écrit, mais aussi les propriétés possibles via cette simple écriture. Commenceons par une propriété simple : l'arité. L'arité d'une relation est le nombre d'élément que la relation lie entre eux. Dans de très nombreux cas, la relation est dite binaire. Une relation est dite binaire quand elle est d'arité 2 (et donc, qu'elle lie 2 objets entre eux, comme "3 est inférieur à 7"). Cependant, avec un peu de réflexion, on peut facilement énumérer des relations d'arité aussi grande que l'on veut.

Les relations d'ordre

Le type de relation qui est probablement le plus utilisé est la relation d'ordre. En effet, une relation binaire est dite "relation d'ordre" quand elle est antisymétrique, réflexive et transitive. Ici, une relation est dite réflexive si, pour tout objet "a", "a" est en relation avec lui même.

\forall a \in E, a ~ a

De plus, une relation est dite antisymétrique si, pour tout objet "a" et "b", si "a" est en relation avec "b" (dans cet ordre précis) et que "b" est en relation avec "a" (dans cet ordre précis), alors "a" est égal à "b". En d'autres termes, si la relation peut s'écrire des deux côtés avec deux objets distincts, alors ils sont égaux.

\forall a, b \in E, a ~ b \land b ~ a \Rightarrow a = b

Si une relation d'ordre est définie sur l'entièreté des éléments d'un ensemble, la relation est dite "totale", et l'ensemble est dit "bien ordonné". Généralement, il est possible de formaliser un ensemble bien ordonné "E" par une relation "~" par un couple constitué de l'ensemble et de la relation.

(E, ~)

Les relations d'équivalences

Les relations d'équivalences sont un type précis de relations mathématiques. En fait, une relation binaire est dite "relation d'équivalence" quand elle est symétrique, réflexive et transitive. Ici, une relation est dite symétrique si, pour tout objet "a" et "b", si "a" est en relation avec "b", alors "b" est en relation avec "a". Ce n'est pas le cas de toutes les relations : pour la relation "plus petit que", 2 n'est pas "plus petit que" 2, mais égal.

\forall a, b \in E, a ~ b \Rightarrow b ~ a

En d'autres termes, l'ordre de "a" et "b" n'importe pas. L'avantage de ce concept est la façon dont on peut l'utiliser. En effet, cette définition complexe est parfaitement équivalente au fait de dire que si deux objets sont en relation, alors ils obéissent à une même propriété quelconque(démontré ici). Cette propriété peut être n'importe quoi, et être de n'importe quelle nature (tant que la relation d'égalité est définie sur les résultats possibles de cette dernière) : "parité", "signe", "chiffre des dizaines"... Ici, nous la notons "f" :

\forall x, y \in E, f(x) = f(y) \Leftrightarrow x ~ y Voici un exemple de propriété, se lisant comme "pour tout x appartenant à un ensemble E, f(x) est vraie si l'ensemble vide appartient à x, et fausse sinon". Nous noterons "~" la relation d'équivalence correspondant à cette propriété. \forall x \in E, f(x) \Leftrightarrow \emptyset \in x \forall x, y \in E, x ~ y \Leftrightarrow f(x) = f(y) Définissons maintenant un "E" précis : E = {{1, A}, {8, D, \emptyset}, {G}, {\emptyset}, \emptyset, {\emptyset, 7}}

Ici, les éléments de "E" obéissant à la propriété "f(x) est vraie" représentent un sous-ensemble de "E", que nous appellerons "F". Tous les éléments de "F" peuvent être reliés par une relation d'équivalence, correspondant ici à la propriété "f".

F = {{8, D, \emptyset}, {\emptyset}, {\emptyset, 7}}

Plein d'autres propriétés peuvent marcher : "cardinal de l'ensemble", "nombres de lettres / nombres dans l'ensemble"... Dans un ensemble quelconque découpé par une relation d'équivalence, la propriété de transitivité permet de dire que, si un élément est reliable à un autre, alors il être reliés à tous les éléments reliables à cet autre objet (et vice-versa). Grâce à ça, nous pouvons définir un objet assez utile : les classes d'équivalences. Une classe d'équivalence d'un élément "x" d'un ensemble "E" représente la classe de tous les éléments de "E" qui peuvent être reliés à "x" par relation d'équivalence "~". Grâce à ce concept, on peut parler de l’entièreté des éléments possédant une propriété avec un seul objet, sans avoir à tous les citer, facilitant les démonstrations et les calculs. D'ailleurs, tous les éléments reliables à "x" peuvent le remplacer, mais n'en garder qu'un est bien plus simple (on choisit généralement le plus simple à utiliser). Ce genre de classe se note en entourant l'élément "x" avec des chevrons.

a \in [x] \Leftrightarrow a ~ x

Dans notre "E" de tout à l'heure, nous pouvons noter la classe d'équivalence à un des éléments de "F" (dont nous choisissons le plus simple) comme ceci :

a \in [{\emptyset}] \Leftrightarrow a ~ {\emptyset} \Leftrightarrow a \in F

Cet outil nous permet de définir une nouvelle opération pour les ensembles : le quotient d'ensemble. Un ensemble quotient d'un ensemble "E" sur une relation d'équivalence "~" est une découpe de "E" entre chaque classe d'équivalence formée par "~" dans "E". En d'autres termes, il s'agit d'une découpe d'un ensemble selon toutes les valeurs possibles d'une de ces propriétés. Nous l'utiliserons énormément pour définir des objets mathématiques (même très simples et intuitifs). Cette notation utilise le symbôle "/". Par exemple, pour un ensemble "E" quotienté par une relation d'équivalence "~", l'ensemble quotient "F" est noté :

F = E / ~

Qu'est ce qu'est une application mathématique ?

En mathématiques, une application est un objet permettant de lier tous les éléments d'un premier ensemble quelconque (nommé ensemble de départ) vers des éléments d'un autre (ou le même) ensemble (nomme ensemble d'arrivée). Une chose très importante : tous les ensembles de l'ensemble de départ doivent être liés à exactement un élément de l'ensemble d'arrivée. À l'inverse, il n'est pas obligatoire que tous les éléments de l'ensemble d'arrivée soit lié à un élément de l'ensemble de départ, ni qu'il ne soit lié qu'à un seul objet (il peut être lié à 2 objets, 3 objets, une infinité...). D'un point de vue rigoureux, une application peut se représenter sous la forme d'un ensemble de couples entre un élément de l'ensemble de départ et un élément de l'ensemble d'arrivée, avec un unique couple pour chaque élément de l'ensemble de départ. Comme tous ces couples sont des couples contenant un élément de l'ensemble de départ et un élément de l'ensemble d'arrivée, il s'agit d'un sous-ensemble du produit cartésien de l'ensemble de départ et d'arrivée (contenant, lui, tous les couples, même ceux qui ne sont pas concernés par l'application). L'ensemble de ces couples formés par l'application est nommé le "graphe" de la fonction. Pour une application quelconque "f" ayant comme ensemble de départ "A" vers l'ensemble d'arrivée "B", on dit que "f" est une application allant de "A" vers "B", et l'on note :

f : A ⟶ B

D'un point de vue logique, la notation est assez basique. Pour une traduction mathématique - français, lisez "pour tout élément x de l'ensemble de départ A, il existe un unique élément y de l'ensemble d'arrivé B, tel que le couple x et y appartiennent au graphe Gf de la fonction".

\forall x \in A, \exists! y \in B, (x, y) \in G_{f}

Pour tout objet "x" appartenant à A, l'objet lié à "x" selon l'application "f" est nommé image de "x" par "f", et se note ainsi :

x ⟶ f(x)

Pour faire le lien avec notre notation logique d'au dessus, "y" représente en fait "f(x)".

\forall x \in A, \exists! y \in B [ y = f(x) \land (x, f(x)) \in G_{f}]

En général, l'ensemble de tous les éléments de l'ensemble d'arrivée appartenant à (au moins) un couple avec un élément de l'ensemble de départ par l'application "f" est nommé "ensemble image de f". Cependant, il est aussi possible de simplement l'appeler "image de f", qu'il ne faut absolument pas confondre avec "l'image de x par f". Pour des raisons de simplicité, nous continuerons à parler d'ensemble image.

Si besoin, il est possible d'expliciter "f(x)" sous la forme d'une expression précise. Généralement, quand une application est explicitée, elle donne une façon de modifier la valeur "x" pour obtenir la valeur de l'ensemble d'arrivée liée à "x" selon cette application. Il n'est pas obligatoire qu'une fonction soit explicité, mais très conseillé pour pouvoir plus facilement savoir quel élément de l'ensemble de départ est lié à quel élément de l'ensemble d'arrivée. Dans ce cas, on peut noter la façon dont "x" est modifié par "f". Voici un exemple dans le cas où "x" est un nombre entier naturel (que nous nous permettons d'utiliser ici pour l'exemple, bien que nous ne les avons pas encore correctement définis), et "f(x)" aussi :

f(x) = 2 * x

Il faut faire attention à une chose : "f(x)" est un objet appartenant à l'ensemble d'arrivée, et "f" est un objet représentant l'application que l'on étudie (et donc, il faut faire attention à utiliser la bonne notation à chaque fois). Une façon très utilisé pour représenter ce concept est celui de diagramme sagittal, où l'on peut lier graphiquement les éléments un à un entre les deux ensembles. Voici un exemple en bas pour l'application allant de "{0, 1, 2, 3, 4}" vers "{0, 2, 4, 6, 8}", transformant "x" en "2 * x":

Un concept assez similaire est le concept de fonction. En mathématiques, une fonction est un objet permettant de lier les éléments de deux ensembles quelconques entre eux, sans obligatoirement que tous les éléments de l'ensemble de départ soit utilisés. Il s'agit d'une définition légèrement moins forte que celle de l'application. En plus, une application est une fonction où tous les objets de l'ensemble de départ sont liés à un unique élément de l'ensemble d'arrivée. Il est néanmoins possible d'obtenir l'ensemble de toutes les valeurs de l'ensemble de départ de la fonction qui sont bel et bien utilisées par cette dernière : cet ensemble se nomme ensemble de définition. Cependant, le point commun est qu'une fonction ne permet de lier un objet de l'ensemble de départ que avec un maximum de un objet de l'ensemble d'arrivée. Voici un exemple de diagramme sagittal de fonction :

Injections, surjections et bijections

Il existe trois types d'applications majeures : les injections, les surjections et les applications.

Commençons par le commencement : l'injection. Une injection est une application mathématique où tous les éléments de l'ensemble de départ sont reliés à au plus 1 objet (soit à 1 objet précisément, soit à aucun objet).

D'un point de vue mathématique, on peut en déduire quelque chose d'intéressant : chaque élément de départ est lié à un objet, et chaque élément d'arrivée est relié à, au maximum, un élément de départ. Donc, si deux objets "a" et "b" ont la même image par une injection, alors ils sont égaux (et la réciproque est vraie dans le cas des antécédents). Cette définition est généralement la définition utilisée pour parler des injections. Dans les formules juste en bas, la première ligne représente la définition de l'application, la deuxième ligne représente la première définition que nous avons vue, et la troisième représente la deuxième que nous avons vue. Le passage de l'une à l'autre (sous forme d'équivalence) est démontré juste ici.

f : E ⟶ F, x ⟶ f(x)

\forall z \in F, [\exists! x \in E, f(x) = z \lor (\exists x \in E, f(x) = z)]

\forall x, y \in E, f(x) = f(y) \Leftrightarrow x = y

Le dernier type est donc la bijection. Une bijection est une application qui est en même temps surjective et injective. D'un point de vue rigoureux, la définition d'une bijection mélange donc celle de l'injection et celle de la surjection. Dans une bijection, chaque élément de départ a un antécédent, et chaque élément d'arrivée a une image (démontré juste ici).

Mathématiquement, une bijection "f" allant de "B" vers "A" se présente ainsi :

f : A ⟶ B, a ⟶ b

\forall b \in B, \exists! a \in A, f(a) = b

Il est d'ailleurs à noter qu'une composition de deux bijections (de "E" vers "F" et de "F" vers "G") donne une nouvelle bijection, de "E" vers "G" (démontré ici). Dans un ensemble "E", il existe une bijection (allant de "E" vers "E") qui, à chaque élément "x" de "E", lui associe... "x" (et donc, qui ne représente pas une modification de l'ensemble à proprement parlé) : cette bijection est nommée application identité de "E". On l'a note généralement avec les deux lettres "Id", et avec l'ensemble "E" en indice. Toute seule, elle ne sert pas à grand chose, mais elle peut être utile pour exprimer formes précises, où l'on veut faire transparaître qu'une forme n'apporte pas de modifications à un ensemble. Par exemple, si la composition d'une application "f et d'une autre application "g" donne l'identité, alors "g" est nommée l'application réciproque de "f". Là est une propriété intéressante : si une application est la réciproque d'une autre, alors elle "annule" l'application de départ (par la composition). Cela permet une autre définition équivalente des bijections : toute bijection admet une application réciproque (elle aussi une bijection), et tout application qui admet une application réciproque est une bijection(démontré juste ici).. Voici la définition (et une illustration) de l'application identité :

{Id}_{E} : E ⟶ E, x ⟶ x

En tout, il existe "n!" bijections différentes ("n!" est un nombre précis, que nous définirons plus tard pour tous ceux qui ne le connaissent pas). D'ailleurs, il existe des ensembles pour lesquelles il ne peut pas exister de bijections entre eux, par exemple si ils ont une taille différente. Cependant, si il existe une bijection entre deux ensembles "E" et "F", ces ensembles sont dit équipotents.

Un type assez utile de bijection est la permutation. Une permutation (aussi appelé substition dans certains vieux ouvrages) est une bijection où l'ensemble de départ est le même que l'ensemble d'arrivée. En effet, dans ce cas, on peut la représenter comme un réarrangement des éléments de l'ensemble, ce qui est généralement le cas des objets "permutations" dans le langage courant. D'ailleurs, l'application identité sur "E" est une permutation sur "E". Il s'agit en fait de la permutation... qui ne modifie aucun élément de "E" (dans le langage courant, il ne s'agirait plus d'une permutation, mais en mathématique, cela en reste une, car la définition est toujours respectée).

{Id}_{E} : E ⟶ E, x ⟶ x

Généralement, la notation d'une transposition dans un ensemble fini de taille "n" représente la façon dont les éléments sont échangés. En fait, on les note sous la forme de deux objets l'un sur l'autre, où l'objet dans haut représente un numéro pour chaque élément de l'ensemble, et l'objet dans bas représente le nouvel arrangement de l'objet après le passage de la permutation. Il est fortement conseillé de noter les premiers éléments de "1" à "n" si possible, pour des raisons de simplicité.

\begin{matrix} (1, 2, 3, 4, 5) \\ (4, 2, 5, 1, 3) \end{matrix}

Il existe cependant une autre notation, plus courte mais un peu plus complexe, dite "notation canonique". En fait, cette notation consiste à noter un élément, puis à noter à sa droite l'élément auquel la permutation le permute, et faire de même avec cet élément (en prenant l'élément de même nombre dans l'ensemble de départ) jusqu'à retomber sur l'élément de départ. Cependant, il est possible que des éléments soit ignorés, si ils ne permutent pas avec un élément de départ, ou avec un des éléments suivants. Dans ce cas, on refait cela avec les éléments manquant jusqu'à qu'il n'en manque plus, en séparant chaque itération par des parenthèses. Dans le cas de notre permutation test, nous devons lire, une transposition est une permutation qui n'échange que deux éléments de l'ensemble entre eux (et ne touche pas aux autres).

\begin{matrix} (1, 2, 3, 4, 5) \\ (1, 2, 5, 4, 3) \end{matrix} = (3 5)

De plus, une permutation est dite circulaire si elle permute une partie de l'ensemble de départ en avançant (ou reculant) chaque élément de cette partie (de telle manière que le dernier élément prenne la place du premier élément si besoin), et ne modifie pas les éléments or de cette partie.. Il s'agit juste de bouger dans un sens et d'une unité une partie de l'ensemble, et de déplacer tous ces éléments de la même manière. Comme le dernier élément prend la place du premier à chaque fois, réaliser une même permutation circulaire autant de fois que la taille de la partie revient à ne pas modifier l'ensemble (tous les éléments auront repris leur place).

\begin{matrix} (1, 2, 3, 4, 5) \\ (4, 1, 2, 3, 5) \end{matrix} = (1 2 3 4)

(1 2 3 4)^{4} =_{Id E}

La composition de fonction et d'application

L'opération la plus simple avec les fonctions (et les applications) est la composition. La composition de fonctions (ou d'applications, ce qui est moins commun mais parfaitement possible) est une opération agissant sur des fonctions / applications, prenant deux fonctions / applications de bases et permettant d'obtenir une nouvelle fonction / / application, admettant comme ensemble de départ l'ensemble de départ de la première fonction, comme ensemble d'arrivée celui de la deuxième fonction, et liant les éléments de l'ensemble de départ aux éléments transformés par la première fonction, puis par la deuxième fonction. L'idée est donc d'utiliser une fonction (ou une application), puis une autre après celle-ci. Voici un exemple de deux fonctions "f" et "g" quelconques, et d'une fonction "h" représentant la composée de "f" et "g".

f : A ⟶ B

f : x ⟶ f(x)

g : B ⟶ C

f : y ⟶ g(y)

h : A ⟶ C

h : z ⟶ f(g(z))

Ici, on peut écrire "h" comme le résultat de l'opération "composition" appliqué sur ces fonctions, opération s'écrivant avec un petit rond :

h = f \circ g

On peut faire de même avec "h(x)".

h(x) = (f \circ g)(x) = f(g(x))

Le diagramme sagittal de "h" peut se représenter comme cela :

D'un point de vue définitionnel, il y a un détail à prendre en compte : la comptabilité de l'ensemble de départ de "g" et de l'ensemble d'arrivée de "f". En effet, l'ensemble image (bel et bien image, pas d'arrivée) de "g" doit obligatoirement posséder un élément en commun avec l'ensemble de définition de "f". Sinon, tous les éléments de l'ensembles de départ n'ont aucune image, et la fonction... n'existe pas.

Dans le cas où l'on compose pour obtenir une application, c'est encore plus strict : l'ensemble image de "g" doit obligatoirement être inclu dans l'ensemble de définition de "f"(sinon, des éléments de l'ensemble de départ peuvent n'avoir aucune image, ce qui est contraire à la définition). C'est d'ailleurs pour éviter cette rigidité que l'on compose en général des fonctions plutôt que des applications.

Introduction à l'arithmétique

L'arithmétique élémentaire

Qu'est ce qu'est l'arithmétique ?

Souvent, quand vous demandez à quelqu'un sa définition des mathématiques, il est fort probable que sa définition ne soit pas celle des mathématiques générales... mais celle de l'arithmétique. En effet, l'arithmétique est la branche des mathématiques étudiant les nombres communs (entiers, rationnels et réels). Bien que cette partie n'est peut être pas la plus importante en mathématiques abstraites, il me semblait important de l'ajouter au premier cours, pour directement faire le lien "logique - nombres". De plus, elle permet de nous donner un premier objet définie "dans le marbre" pour présenter des concepts plus complexes, qui auront besoin d'une très grande rigueur.

Comme pour la théorie des ensembles, l'arithmétique a subit de nombreux remaniement pendant son histoire. Historiquement, on retrouve déjà des traces d'études précises des nombres 1000 ans avant J.C.,via les phéniciens. Plus récemment (dernier millénaire avec J.C.), les grecs se sont aussi emparés de l'affaire, avec de très grands noms : un mec intelligent, un mec intelligent, un mec intelligent...

Axiomatiquement définir les nombres entiers naturels

Historiquement, définir précisément les nombres entiers naturels n'a pas été une mince affaire. Au début (de l'histoire humaine), un nombre entier naturel représentait une quantité précise d'un certain objet, que l'on peut donc compter. Cette définition est très concrète (avec la notion d'objet à compter), bien que l'abstraction apparaitra petit à petit avec l'invention d'une notation précise pour les nombres. D'un point de vue notationnelle, les nombres ont longtemps étaient notés de manière très concrète, comme le nombre de points que représentait le nombre en question(c'est le cas des nombres hiéroglyphes égyptiens ou des os d'Ishango). Cependant, des systèmes plus abstraits utilisant des symbôles à la place de dénombrage apparaissent des l'arrivée des sumériens, avec leur système base 60, et chez les civilisations suivantes : grecques, romains... Le grecs un mec intelligentles défini comme une collection d'objets unitaire (valant 1). Dans ce cas, l'addition (et, globalement, toutes propriétés des nombres entiers naturels) est très facilement définie, en rapprochant physiquement deux collections d'objets représentant les nombres à additionner. Pendant longtemps, le nombre "zéro" n'était pas normalisé comme étant un nombre entier naturel, et son utilisation de la sorte dépend des auteurs. Cependant, l'arrivée de la logique avancée à la fin du XIXème siècle va forcer les mathématiciens à vouloir axiomatiser tout ça. Pour cela, de nombreux mathématiciens tentent des choses : un mec intelligent, un mec intelligentavec son système d'axiome précis, un mec intelligent... La célèbre théorie des ensembles ZFC (que l'on a déjà présenté plus tôt dans ce cours) offre un axiome permettant de les définir : l'axiome de l'infini. L'arrivée de la crise des fondements va bouleverser toutes ces définitions, mais cela ne va pas arrêter les mathématiciens ayant travaillé dessus.

Grâce à la théorie des ensembles ZFC, on peut axiomatiquement définir l'ensemble des nombres entiers naturels, comme étudié au collège. Pour cela, nous allons utiliser l'axiome de l'infini. Pou rappel, l'axiome de l'infini stipule qu'il existe un ensemble contenant un élément de départ nommé "0", et tel que tous les éléments "n" de cet ensemble admettent un élément précis (défini via une fonction), nommé "successeur de n" ou "successeur(n)". Donc, cet ensemble contient "successeur(0)", "successeur(successeur(0))"... En fait, cet ensemble se comporte exactement comme l'ensemble des nombres entiers naturels, noté "N". En effet, on peut définir "successeur(0) = 1", "successeur(successeur(0)) = 2"... D'un point de vue vocabulaire, il est parfaitement évident que le successeur de 0 est 1, que celui de 1 est 2, que celui de 56 est 57...

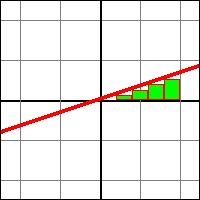
De plus, on peut trouver que ce fameux "successeur" est une application bijective de "N" vers "N sans 0" (démontré ici par récurrence). Dans ce cas, il existe une application réciproque à "successeur" allant de "N sans 0" vers "N", que nous nommerons "prédécesseur".

Pour manipuler les nombres entiers naturels, il existe un élément de syntaxe très pratique : l'opération. Une opération est une action où, grâce à une (ou plusieurs) valeur de départ (nommée opérande), on y définit une égalité représentant une (ou plusieurs) valeurs traitées via les valeurs de départs. Cette définition est très générale, car souvent, la définition précise du mot "opération" est ambiguë. Cependant, une opération (comme "2 + 3") n'est pas une proposition, et donc pas une relation, bien qu'il soit courant de mettre en relation une opération avec un résultat juste, ou non (comme "2 + 3 = 5", qui est une relation juste). Généralement, une opération prend 1 ou 2 éléments en entrée. Les cas les plus célèbres sont l'addition et la multiplication.

L'opération la plus élémentaire entre deux nombres entiers naturels est l'addition. D'un point de vue rigoureux, une addition entre deux nombres entiers naturels représente une opération entre deux nombres entiers naturels "a" et "b", donnant comme valeur la valeur partant de "a" obtenue après la répétition de "b" fois l'application "successeur". Comme tout le monde le sait, elle se note avec une croix "+". On peut la définir (itérativement) comme ceci :

\forall n \in N, n + 0 = n

\forall n, a \in N, n + successeur(a) = successeur(n + a)

Cette définition est une définition un peu complexe pour parler de l'addition comme nous la connaissons tous. Elle est parfaitement équivalente au fait d'imaginer "x" et "y" objets dans sa tête, de les mettre à côté, et de compter la totalité des nombres, comme appris en petite section.

s = successeur(successeur(0)) + successeur(successeur(successeur(0)))

s = successeur(successeur(successeur(successeur(successeur(0)))))

2 + 3 = 5

Pour tout nombre entier naturel, additionner deux nombres entiers naturels donnera toujours comme résultat un nombre entier naturel(démontré ici par récurrence). Dans le cas où l'un des deux nombres est 0, le résultat de l'opération donne le nombre qui n'est pas 0 (ou 0 si les deux nombres sont 0). De plus, l'ordre de réalisation de plusieurs additions entre elles n'a pas d'importance sur le résultat final (démontré ici par récurrence) : (2 + 3) + 4 = 2 + (3 + 4) = 9.

Dans les mathématiques communes, il est souvent admis que l'addition admet une opération "opposée" : la soustraction. D'un point de vue rigoureux, une soustraction entre deux nombres entiers naturels représente une opération entre deux nombres entiers naturels "a" et "b", donnant comme valeur la valeur partant de "a" obtenue après la répétition de "b" l'application "prédécesseur". Comme tout le monde le sait, elle se note avec une croix "-". Sa définition la plus générale utilise justement l'addition.

\forall a, b \in N, \exists c, a - b = c \Leftrightarrow a = b + c

Attention : comme nous le verrons après, "c" n'est pas forcément un nombre entier naturel ici. La logique derrière cette définition permet de prouver quelques propriétés assez pratique. Par exemple, "a - a = c" équivaut à dire que "a + c = a", et donc que "c" = 0 : soustraire un nombre à lui même donne 0. De plus, elle a la propriété d'annuler l'opération d'addition : si vous additionner "b" à un nombre "a", puis que vous lui soustrayez "b", vous ré-obtenez "a".

\forall a, b \in N, \exists c, a + b - b = c \Leftrightarrow a = c

Comme pour l'addition, cette définition est une définition un peu complexe pour parler de la soustraction comme nous la connaissons tous. Elle est parfaitement équivalente au fait d'imaginer "x" objets dans sa tête, et de retirer "y" objets aux "x" objets, comme appris en petite section. Nous pouvons aussi utiliser cette comparaison pour comprendre la définition générale : imaginez vos "x" objets, si "y" objets représentent moins d'objets que "x" objets, alors vous pouvez imaginer un nombre "c" d'objets qui, quand on les ajoute à "y" objets, donnent "x" objets.

s = successeur(successeur(successeur(0))) - successeur(successeur(0))

s = successeur(0)

3 - 2 = 1 \Leftrightarrow 3 = 2 + 1

Elle pose cependant un problème : que se passe t-il si l'on tente de réaliser l'opération "2 - 3" ? Nous devons appliquer trois fois l'application "prédécesseur" sur 2, soit "successeur(successeur(0))". Si nous l'appliquons une fois, nous obtenons "successeur(0)", et si nous l'appliquons une autre fois, nous obtenons "0". Or, il nous faut encore l'utiliser une fois, ce qui donne "prédécesseur(0)". Or, l'application prédécesseur ne permet d'obtenir des nombres entiers naturels que si l'antécédent est un nombre entier naturel qui n'est pas 0. En d'autres termes, "prédécesseur(0)" n'est pas un nombre entier naturel, et donc "2 - 3" non plus. Certaines soustractions donnent des résultats qui ne sont pas des nombres entiers naturels.

La deuxième opération la plus élémentaire entre deux nombres entiers naturels est la multiplication. D'un point de vue rigoureux, une multiplication entre deux nombres entiers naturels représente une opération entre deux nombres entiers naturels "a" et "b", donnant comme valeur la valeur partant de "a" obtenue après la répétition de "b" fois l'opération d'addition de "a" avec lui même. Comme tout le monde le sait, elle se note avec une croix légèrement tourner, comme un x : "*".

\forall n \in N, n * 0 = 0

\forall n \in N, n * 1 = n

\forall n, a \in N, n * successeur(a) = (n * a) + n

Comme l'addition, cette définition est une définition un peu complexe pour parler de la multiplication comme nous la connaissons tous.

s = successeur(successeur(0)) * successeur(successeur(successeur(0)))

s = successeur(successeur(successeur(successeur(successeur(successeur(0))))))

2 * 3 = 6

Pour tout nombre entier naturel, multiplier deux nombres entiers naturels donnera toujours comme résultat un nombre entier naturel(démontré ici par récurrence). Par définition, pour tout nombre entier naturel, le multiplier avec 0 donne 0. Toujours par définition, dans le cas où l'un des deux nombres est 1 (et ou aucun des nombres n'est 0), le résultat de l'opération donne le nombre qui n'est pas 1 (ou 1 si les deux nombres sont 1). Finalement, l'ordre de réalisation de plusieurs multiplications entre elles n'a pas d'importance sur le résultat final (démontré ici par récurrence) : (2 * 3) * 4 = 2 * (3 * 4) = 24.

Une propriété assez intéressante de l'opération multiplication (qui permet en plus de prouver que l'ordre de réalisation de plusieurs multiplications entre elles n'a pas d'importance) est la distributivité. Une opération "." est dite distributive par rapport à une opération "~" lorsqu'il est possible de transformer l'opération "a . (b ~ c)" en l'opération "a . b ~ a . c". En effet, la multiplication est distributive par rapport à l'addition dans les nombres entiers naturels(démontré ici par récurrence).

2 * (3 + 4) = 2 * 3 + 2 * 4 = 14

Si il existe une opération qui "annule" l'effet de l'addition (la soustraction), il existe aussi une opération qui annule l'effet de la multiplication : la division. D'un point de vue rigoureux, une division entre deux nombres entiers naturels représente une opération entre deux nombres entiers naturels "a" (nommée le "diviseur") et "b" (nommé le dividende), donnant comme valeur la valeur dont il faut multiplier "b" pour obtenir "a". Généralement, elle se note avec une barre un peu tournée "/". Sa définition la plus générale utilise justement la multiplication.

\forall a \in N, \forall b \in N*, \exists c, a / b = c \Leftrightarrow a = c * b

Il est à noter que le diviseur ne peut pas être nul, pour une raison assez simple : si "b = 0", il n'existe pas de nombre "b" tel que "c * b" ne soit pas égal à 0, et la division est impossible. D'un point de vue notationnel, il est aussi possible de la noter en notant le dividende et le diviseur sur la même colonne, en mettant le dividende au dessus du diviseur, et de de séparer les deux par une barre.

\forall a \in N, \forall b \in N*, \exists c, a / b = c \Leftrightarrow \frac{a}{b} = c

Comme pour la soustraction, "c" n'est pas forcément un nombre entier naturel. Cependant, si "b" est un nombre entier naturel (et que la multiplication existe et fonctionne), "b" est appelé un diviseur de "a" ("a" est dit divisible par "b" et "a" est un multiple de "b"). Dans tous les cas, il est assez simple de voir que 1 est un diviseur de tous les nombres entiers naturel existant, et que chaque nombre entier naturel est divisible par lui même. De manière réciproque, tous les nombres dans "N" sont des multiples de 1. De plus, tous les multiples d'un certain nombre entier naturel "n" forment un ensemble, représentant un sous-ensemble de "N", et généralement noté "aN" (comme "2N", "3N", "18N"...).

De plus, nous pouvons définir deux relations d'ordres précises dans l'ensemble des nombres entiers naturels : supérieur et inférieur. Un nombre entier naturel "a" est dit strictement supérieur à un nombre entier naturel "b" si nous pouvons obtenir "a" en appliquant une ou plusieurs fois la fonction successeur (en additionnant 1) à "b". Dans ce cas, "b" est dit strictement inférieur à "a". Cette définition est parfaitement équivalente au fait d'imaginer "a" et "b" objets dans sa tête, de les mettre à côté, et de dire que "a" objets représente plus d'objets que "b" objets. La relation "strictement supérieur" se note avec un chapeau tourné vers la droite, et la relation "strictement inférieur" avec un chapeau tourné vers la gauche :

\forall a, b \in N, a > b \Leftrightarrow \exists c \in N*, a = b + c

\forall a, b \in N, a > b \Leftrightarrow b < a

successeur(successeur(0)) > successeur(0)

successeur(0) < successeur(successeur(0))

2 > 1

1 < 2

Une autre relation similaire existe : supérieur ou égal et inférieur ou égal. Un nombre entier naturel "a" est dit supérieur ou égal à un nombre entier naturel "b" si "a" est supérieur à "b" ou si "a" est égal à "b". C'est pour cela que nous éviterons d'utiliser les termes supérieur ou inférieur seules : on risque de se tromper d'opérateur. La relation "supérieur ou égal" se note avec un chapeau tourné vers la droite sous ligné, et la relation "inférieur ou égal" avec un chapeau tourné vers la gauche sous ligné :

\forall a, b \in N, a \geq b \Leftrightarrow \exists c \in N, a = b + c

successeur(successeur(0)) \geq successeur(0)

successeur(successeur(0)) \geq successeur(successeur(0))

successeur(0) \leq successeur(successeur(0))

successeur(successeur(0)) \leq successeur(successeur(0))

2 \geq 1

2 \geq 2

1 \leq 2

2 \leq 2

Bien évidemment, il existe une démonstration précise de pourquoi ces relations sont des relations d'ordres (énumérées ici). D'ailleurs, l'ensemble des nombres entiers naturels est bien ordonné par ces 4 relations. On peut aussi facilement prouvé (et déduire) que, si deux nombres entiers naturels "a" et "b" vérifient la relation "a est supérieur ou égal à b", alors "a - b" est un nombre entier naturel (démontré ici). De plus, avec ces nombres entiers naturels, ces 4 relations permettent de former des équivalences via l'addition et la multiplication(sauf dans le cas où l'on multiplie par 0 pour les relations "strictement inférieur" et "strictement supérieur") :

\forall a, b, c, d \in N, a < b \Leftrightarrow a + c < b + c \Leftrightarrow a * d = b * d

\forall a, b, c, d \in N, a > b \Leftrightarrow a + c > b + c \Leftrightarrow a * d = b * d

\forall a, b, c, d \in N, a \leq b \Leftrightarrow a + c \leq b + c \Leftrightarrow a * d = b * d

\forall a, b, c, d \in N, a \geq b \Leftrightarrow a + c \geq b + c \Leftrightarrow a * d = b * d

Axiomatiquement définir les nombres entiers relatifs

Comme nous l'avons vue, si l'opération "2 - 3" est possible chez les nombres entiers naturels, alors l'objet "prédécesseur(0)" doit être un nombre entier naturel, ce qui n'est pas le cas. Cependant, il existe un ensemble de nombres similaire à N qui permet cette propriété : les nombres entiers relatifs. Les nombres entiers relatifs représentent une extension de l'ensemble des nombres entiers naturels, rajoutant des nombres inférieur à 0, nommés nombres négatifs. Ces nombres négatifs sont notés exactement comme des nombres entiers naturels, avec le symbole "-" juste avant. À l'inverse, les nombres supérieurs à 0 sont nommés nombres positifs, et peuvent se noter avec le symbole "+", ou plus communément sans symbole. Ces symboles "+" et "-" utilisées avec un nombre entier relatif sont nommés le signe du nombre entier relatif.

-2, -1, 0, 1, 2

La seule ambiguïté ici est le signe de "0" : il peut théoriquement représenter les deux signes, mais pour des raisons de facilité, on va dire que "+0 = -00", et nous allons privilégier le signe "+". D'ailleurs, il est possible de définir ce signe sous la forme d'une application allant de l'ensemble des nombres entiers naturels à {"+", "-"}, généralement notée "sign". Pour bien comprendre cette définition, il ne faut plus voir les nombres comme des quantités, mais comme des "distances" à 0. Ici, la distance entre deux nombres entiers relatifs "a" et "b" représente le nombre de déplacement nécessaire de "a" pour atteindre "b". Avec cette façon de voir les choses, nous pouvons construire l'ensemble des nombres entiers relatifs comme une ligne. Sur cette ligne, on place un point "0" au milieu, les nombres positifs à droite, et les nombres entiers négatifs à gauche. Bien évidemment, ils sont placés à une distance de zéro correspondant à leur nombre.

D'ailleurs, cette "distance" à 0 d'un nombre entier relatif est nommée la valeur absolue de ce nombre entier relatif. Il est possible d'écrire cette valeur absolue sous la forme d'une application de l'ensemble des nombres entiers relatifs vers l'ensemble des nombres entiers naturel, généralement noté "abs". En effet, chaque nombre entier relatif ne possède qu'une unique distance à 0 : chaque antécédent à bien une image. Dans ce contexte là, l'opération soustraction de nombres entiers relatifs prend tout son sens. En effet, soustraire deux nombres entiers relatifs "a" et "b" revient à trouver la distance entre eux, positive si nous devons aller vers la gauche, et négative si on doit aller vers la droite. Cette définition est équivalente à dire que la soustraction nous permet de bouger d'un certain nombre, pour aller à "b" en partant de "a" (positif si nous allons vers la gauche, et négatif si nous allons vers la droite). À l'inverse, additionner deux nombres entiers relatifs "c" et "d" revient à aller à "c", et de bouger de "d" unités vers la droite si le nombre est positif, et de "d" unités à gauche si le nombre est négatif.

La définition "logique" standard des nombres entiers relatifs (que nous utiliserons pour les démonstrations) est un peu complexe. L'idée est de définir les nombres entiers relatifs comme un couple de nombres entiers naturels, dont la soustraction du plus grand au plus petit donne la valeur absolue du nombre, et où l'ordre (plus grand en premier ou en deuxième) donne le signe du nombre. Pour être précis, si le plus grand est en premier, alors le nombre est positif, sinon il est négatif. En fait, il s'agit de manière intuitive du nombre résultant de la soustraction du second terme au premier terme.

a = (4, 2) \Leftrightarrow a = 4 - 2 \Leftrightarrow a + 2 = 4 \Leftrightarrow a = 2

b = (1, 4) \Leftrightarrow b = 1 - 4 \Leftrightarrow a + 4 = 1 \Leftrightarrow b = -3

c = (e, f) \Leftrightarrow c = e - f \Leftrightarrow c + f = e

Dans ce cas, nous pouvons définir l'ensemble des nombres entiers relatifs (noté "Z", en référence au mot "zahlen" représentant le mot "nombres" en allemand) comme le produit cartésien de N et N. Le problème : les nombres peuvent être représenté par plusieurs couples, et ne sont pas uniques. Par exemple, 2 peut être (4, 2), mais aussi (2, 0). Pour éviter ce problème et rendre chaque nombre entier relatif unique, nous devons indiquer que les couples donnant le même nombres sont parfaitement égaux, grâce à une relation d'équivalence. Pour faire notre relation d'équivalence, nous allons utiliser une propriété déduite la définition de la soustraction dans les nombres entiers naturels (qui sont les constituants de notre couple) :

\forall a, b \in N, \exists e, a - b = e \Leftrightarrow a = b + e

L'idée est donc de comparer deux soustractions, et d'ajuster la formule pour en obtenir une propriété parfaitement définie (avec de simples additions de nombres entiers relatifs). Ici, nous allons noter cette relation d'équivalence "~", et nous pouvons proprement définir l'ensemble des nombres entiers relatifs comme le produit cartésien de N et N quotienté par "~".

(a, b) ~ (c, d) \Leftrightarrow a - b = c - d \Leftrightarrow a + d = b + c

Z = (N * N)/~

Grâce à cette relation d'équivalence, il est très facile de voir que tous les nombres de la forme "(a, 0)" (et donc, de la classe d'équivalence "[(a, 0)]") représentent en fait le nombre entier naturel "a". En réalité, nous n'allons utiliser cette définition que pour quelques propriétés ultra basiques de "Z", mais jamais ailleurs. D'ailleurs, cette définition nous permet de démontrer que l'application "abs" est bien une application (pour rappel, le résultat d'une addition / soustraction est unique). Donc, on peut aussi y définir les exactes mêmes opérations que dans "N". Par exemple, on peut y définir l'opération successeur : comme le successeur de "a" est "successeur(a)" (ou a + 1), le successeur de "(a, 0)" est donc "(successeur(a), 0)" (ou "(a + 1, 0)"). Prolongeons cette application dans tous "Z" : pour tous nombres "a" de "Z" écrit sous la forme "(b, c)" avec "b" et "c" des nombres entiers naturels, le successeur de "a" est "(successeur(b), c)".

Comme pour l'ensemble "N", nous pouvons facilement définir l'addition et la multiplication dans "Z". L'addition entre deux nombres entiers relatifs "a" et "b" est extrêmement simple à définir.

\forall a, b \in Z, \exists c, d, e, f \in N, a = (c, d), b = (e, f), a + b = (c + e, d + f)

Ici, les crochets nous permettent d'utiliser les classes d'équivalences, pour généraliser le calcul. En fait, il ne nous suffit qu'à additionner dans "N" les composants de "a" et "b". On peut vérifier ce calcul sans problème, avec un exemple concret.

a = -5 = (5, 10), b = 2 = (6, 4)

a + b = (11, 14) = -3

Tous ceux qui connaissent les nombres entiers naturels peuvent le constater : ce calcul est parfaitement juste. L'avantage, c'est que les propriétés de l'addition dans "Z" sont très faciles à déduire grâce aux propriétés de l'addition dans "N". On peut donc le vérifier sans problèmes : toute addition dans "Z" donne un élément de "Z", l'ordre de réalisations de plusieurs additions n'importe pas, et l'ordre des opérandes non plus (démontré ici).

De plus, comme pour l'application "successeur", on peut aussi définir "prédécesseur" dans "Z". Selon la définition vue plus haut, comme le prédécesseur d'un nombre entier naturel "a" est "prédécesseur(a)", le prédécesseur de "[(a, 0)]" devrait être "[(prédécesseur(a), 0)]". Cette définition est inutile (elle ne change pas le problème), mais permet d'ouvrir la voie à une autre définition bien plus intéressante. En effet, si un nombre entier relatif est défini sous la forme "(b, c)" avec "b" et "c" des nombres entiers naturels, et que seul la différence entre "b" et "c" changent le nombre, on peut changer cette différence sans sortir de la zone de définition d'aucune des applications. Effectivement, la valeur "(prédécesseur(b), c)" est parfaitement équivalente à la valeur "(b, successeur(c))". On peut le démontrer en maniant correctement les identités conséquences de la définition d'un nombre entier relatif.

\forall d \in Z, d = (prédécesseur(b), c) \Leftrightarrow d + c = prédécesseur(b) \Leftrightarrow successeur(d + c) = b \Leftrightarrow c + successeur(d) = b \Leftrightarrow c = (b, successeur(c))

Tout cela permet quelque chose de très utile : on peut définir la soustraction dans "Z" directement via l'addition. Pour rappel, la soustraction est définie grâce à l'application "prédécesseur", qui ne prend des valeurs que dans les nombres entiers naturels strictement supérieurs à 0. Or, nous pouvons nous débrouiller pour redéfinir la soustraction de manière plus utilisable. Imagineons 2 nombres entiers relatifs "a" et "b" (toujours de la forme "a = (c, d)" et "b = (e, f)") que nous souhaitons soustraire. Selon la définition de la soustraction, nous devons utiliser l'opération prédécesseur "e - f" fois sur "c" pour obtenir la valeur adéquat. Cependant, comme nous l'avons démontré, cela est parfaitement équivalent à utiliser l'opération successeur "e - f" fois sur "d". Par définition d'un nombre entier relatif, cela consiste à additionner "e" à "d" et "f" à "c". Hors, un problème subsite : comment ne pas avoir de problèmes avec "e - f" ? L'explication est assez simple : l'idée de la soustraction est de définir une distance entre deux nombres, ici "e" et "f", que l'on peut obtenir dans tous les cas. Dans ce cas, si "e" est plus grand que "f", alors il n'y a aucun problème à appliquer la dernière définition de la soustraction vue, mais dans le cas inverse, il faut innover. En fait, si "e" est inférieur à "f", nous devons utiliser l'opération successeur "f - e" fois sur "c". Par définition d'un nombre entier relatif, cela consiste à additionner "e" à "d" et "f" à "c". Ici, une définition semble se tracer : soustraire "a" à "b" revient à obtenir le nombre entier relatif quand on inverse "e" et "f" dans "b", et d'additionner ce nombre à "a".

(4, 9) - (5, 2) = (4, 9) + (2, 5) = (6, 14) = -8

D'un point de vue vocabulaire, le nombre entier relatif obtenu quand on inverse "e" et "f" dans "b" est nommé "opposé de b", généralement noté "-b". Selon notre définition des nombres entiers relatifs, on peut assez facilement constater que l'opposé de "b" à l'exact même valeur absolue que "b", avec juste le signe qui change. On peut aussi vérifier une autre identité : additionner "b" est "opposé de b" donne "(0, 0).

(e, f) + (f, e) = (e + f, f + e) \in [(0, 0)] = 0

Maintenant, définissons la multiplication dans "Z". Intuitivement, elle est plus simple à définir, mais un peu plus longue. En fait, la multiplication entre deux nombres entiers relatifs donne comme résultat un nombre entier relatif de valeur absolue représentant la multiplication de celles des deux opérandes. Pour le signe, nous utilisons une règle assez connue, nommé la règle des signes. Le signe de la multiplication entre deux nombres entiers relatifs est positif si les deux opérandes ont le même signe, et négatif sinon.

\forall a, b \in Z, abs(a * b = abs(a) * abs(b)), sign(a * b) = {" + " si sign(a) = sign(b), "-" sinon}

(-3) * (5) = (-15)

(3) * (-2) = (-6)

(3) * (8) = (24)

(-3) * (-4) = (12)

À part la règle des signes, rien ne change vraiment de la multiplication dans "N". Comme pour dans "N", l'ordre de réalisation de la multiplication n'importe pas, et l'ordre des opérandes autour de la multiplication non plus(démontré ici). De plus, on peut facilement déduire que multiplier un nombre entier relatif par "-1" revient à obtenir son opposé.

Finalement, nous pouvons définir les deux mêmes relations d'ordres précises dans l'ensemble des nombres entiers relatifs que dans l'ensemble des nombres entiers naturels : supérieur et inférieur. Dans "Z", un nombre entier positif "a" est supérieur à un autre nombre entier positif "b" si sa valeur absolue est supérieure à celle de "b", et tout nombre entier positif est supérieur à tous nombres entiers négatifs. De plus, un nombre entier négatif "a" est supérieur à un autre nombre entier négatif "b" si sa valeur absolue est inférieur à celle de "b". Donc, le rapport s'inverse quand le nombre est négatif. Comme dans "N", on peut définir de l'exact même façon la relation "inférieur ou égal", "strictement supérieur" et "strictement inférieur". Toute ces définitions permettent bien de garder nos propriétés de relation d'ordre (démontré ici).

3 \geq 2

-2 \geq -3

Les ensembles dénombrables

Les ensembles dénombrables sont une catégorie d'ensembles infinis très précis. Un ensemble infini est dénombrable si il est équipotent (et donc, si il existe une bijection) à l'ensemble des nombres entiers naturels. En d'autres termes (plus simple) : un ensemble infini est dénombrable si il est possible de lister tous ses éléments, comme on listerait les nombres entiers naturels. Voici un exemple, où l'on montre que l'ensemble des nombres entiers naturel pair a le même cardinal que celui... des nombres entiers naturels.

Cette notion est utile, car la notion de "taille" d'un ensemble devient inutilisable pour des ensembles infini. Dans ce cas précis, la notion de cardinal d'un ensemble infini est utile : si un ensemble est dénombrable, on dit qu'il a le même cardinal que N. Le "cardinal de N" se note avec un symbôle assez précis : la lettre de l'alphabet hébreu "aleph", avec comme indice le nombre "0".

א_{0}

Ce concept donne des résultats... assez bizarre. En effet, bien que N soit inclu dans Z, il existe une bijection de N vers Z, exprimable de manière particulièrement simple.

F : N ⟶ Z

n ⟶ {(-1)}^{n} * \frac{n}{2}

Cette bijection est assez simple : si "n" est pair, "-1 exposant n" est positif, sinon il est négatif. Grâce à ça, on peut aller dans les positifs, comme dans les négatifs. En suite, on multiplie cette valeur par la partie entière (vers le haut) de n divisé par 2. Donc, pour un nombre impair puis pair consécutif, n divisé par 2 a la même valeur. Donc, on peut aller dans les positifs et leur attribuer une valeur, puis dans les négatifs et leur attribuer l'exact même valeur (opposé, bien évidemment). Successivement, on y attribue toutes les valeurs possibles dans Z.

De plus, N et N X N sont équipotents, et donc ont le même cardinal. Il existe une bijection assez simple à comprendre entre N et N X N : la fonction de couplage de Cantor.

Si ce concept existe, on peut en déduire le concept opposé : les ensembles infinis indénombrables. Un ensemble infini est indénombrable si il n'existe pas de surjections sur l'ensemble des nombres entiers naturels (il existe des éléments qui ne sont pas reliables à un nombre entier naturel). C'est le cas des nombres réels. Imaginez cette disposition de nombres réels, où nous les considérons dénombrables.

Nous pouvons trouver un nombre (en rouge), qui est un nombre réel. Maintenons, prenons le nombre où l'on rajoute 1 au chiffre de tous les chiffres après la virgule du nombre rouge (sans exceptions, où l'on met un "0" si l'on croise un "9"). Ce nombre est un nombre réel, il devrait donc être quelque part dans ce tableau. Or, il ne peut pas être le premier nombre : sa première décimale après la virgule est différente. Il ne peut pas être le deuxième nombre : sa deuxième décimale après la virgule est différente. Il ne peut pas être le n-ième nombre : sa n-ième décimale après la virgule est différente. Donc, il existe un nombre réel qui ne peut pas être ici : l'ensemble des réels n'est pas dénombrable. Le cardinal de l'ensemble des nombres réels est souvent noté "2 exposant aleph 0" :

2^{א0}

En utilisant le théorème de Cantor, on peut prendre comme exemple l'ensemble des parties de N, qui est indénombrable.