L'algorithme de traçage du cercle

Algorithme de traçage d'ellipses
La complexe conversion géométrie - informatique
Les bases géométriques nécessaires
Cette algorithme repose sur de la géométrie, beaucoup de géométrie. Pour rappel, nous avons une section entière du site qui est dédiée à la géométrie. Cependant, rappelons quelques définitions. Un cercle est une figure géométrique 2D, tel que tous ses points se trouvent à une distance similaire (appelée "rayon" du cercle) d'un même point, dit "centre" du cercle. C'est la forme la plus simple de l'ellipse, bien qu'il n'en soit pas une généralité. En géométrie pure, une ellipse est une figure géométrique 2D résultant de la projection d'un cône 3D sur un plan 2D passant par son axe de rotation, sans passer par le sommet, ni être coplanaire à la base du cône. De manière plus simple, purement 2D et suffisante dans notre contexte, une ellipse est un cercle étiré sur un de ces axes (X ou Y). Théoriquement, un cercle n'est pas une ellipse, car un cercle est aussi une projection d'un cône sur un plan 2D, mais avec un plan coplanaire à la base du cône. Cependant, il existe un terme mathématique réunissant les deux mondes (ainsi que les points / segments, aussi obstensibles de cette manière) : l'ellispe dégénérée. Dans la suite, sauf contre-indication, le terme ellipse correspondra à l'ellipse OU au cercle.
Une autre notion assez connue est celle de cercle trigonométrique. Pour rappel, le cercle trigonométrique est un cercle de rayon 1 et de centre le repère du plan, permettant de facilement définir les fonctions trigonométriques. Grâce aux propriétés de ce cercle, nous allons facilement pouvoir tracer le cercle. De plus, nous pourront concevoir un lien entre le cercle trigonométrique et une "ellipse" trigonométrique, qui nous sera aussi très utile.
Le cahier des charges de l'algorithme
Ici, l'algorithme sera coupé en 3 parties :
- Traçage de cercle / ellipse
- Traçage d'une bordure au cercle
- Délimitation du cercle
- Rotation de l'ellipse
Ces tâches sont triées de la même manière qu'elles ont était conçues.
Le traçage du cercle
L'idée du traçage
Ici, l'algorithme va dresser une liste des pixels à colorer pour le cercle, puis les colorer
L'étape complexe ici est l'obstention des coordonnées des pixels nécessaires. C'est ici que la trigonométrie nous sera classique. Déjà, posons quelque chose : nous allons considérer l'image comme une suite de pixels, les uns à côté des autres. Dans cette image, nous allons tracer un segment, représentant le diamètre du cercle à son milieu.
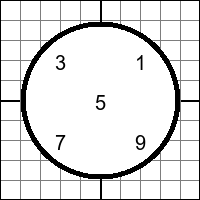
En suite, nous allons parcourir cette ligne de gauche à droite, et obtenir la hauteur nécessaire pour le tracé du cercle pour chaque position X. Grâce à ça, le cercle sera tracé dans son intégralité sans problème. Cette opération demande un peu de mathématiques. En effet, pour chaque parcours de la ligne, nous prenons une position "X" différente par rapport au milieu du cercle (allant de 0 jusqu'au rayon du cercle). Grâce à ça, nous pouvons définir un triangle rectangle, avec un côté représentant la position "X" nécessaire, un autre représentant le "Y" nécesasire (que l'on cherche), et l'hypothénus représentant le rayon du cercle, comme dans le cercle trigonométrique. Avec ça, nous pouvons utiliser les formules classiques de trigonométrie. Ici, l'obstention de l'angle nécessaire pour le point du cercle à un "X" donné s'obtient en passant le quotient de ce "X" et de l'hypothénus (le rayon du cercle) à la fonction "arcosinus". En suite, l'obstention du "Y" nécessaire se fait en multipliant le sinus de l'angle obtenu par le rayon du cercle.
Ici, on obtient le "Y" au dessus de la ligne que nous avons tracé précédemment. Or, les propriétés du cercle nous permettent d'utiliser aussi ces valeurs en dessous, et même à droite du cercle, pour minimiser les calculs. En reportant ces données sur notre tracé, et en colorisant tous les pixels entre les deux pixels obtenus pour chaque "X", on obtient un résultat satisfaisant.
Le cas d'une ellipse
Heuresement pour nous, une grande partie des propriétés du cercle marche avec l'ellipse, à quelques différences près. La différence principale est la différence entre la largeur et la hauteur de l'ellipse. Pour tenir compte de cette différence, nous allons simplement utiliser des rapports de proportionnalités entre les deux tailles (hauteur et largeur). En fait, après l'obstention du "Y", nous avons juste à y multiplier le ratio "vertical / horizontal" (ce qui ne change d'ailleurs pas les calculs de départ).
L'ajout d'une bordure
Légèrement modifier les calculs
Ici, l'idée est de réserver une quantité précise de pixels à la partie externe de l'intérieure du cercle pour tracer une bordure. L'idée la plus "simple" est de tracer un plus petit cercle / ellipse dans un de taille demandée, pour laisser la partie bordure au plus gros cercle. Or, cette technique demande deux traçages de cercles, donc très peu optimisé. À la place, nous allons modifier un peu les calculs, pour tracer la bordure. Ici, l'idée est assez simple : pour chaque "X", on va calculer les angles correspondant (avec la technique vue plus haut) du cercle bordure inclue, et du cercle bordure exclue. Comme l'un est plus large que l'autre, les deux cercles auront donc des mesures différentes, et des angles différents. Le calcul du rayon du cercle sans bordure est extrêmement simple (et logique).
Ici, "Rx" est le rayon du cercle sans bordure, "r" est le rayon du cercle avec bordure, et "b" est la taille de la bordure. Or, bien que l'angle change selon le "X" actuel, le rayon des cercles ne changent pas (ou du moins, leur changement est parfaitement calculable avec le "X" seul). Donc, nous allons calculer la différence entre les deux cercles pour le "X" actuel (représentant la taille de la bordure à ce "X"), grâce au théorème d'Al-Kashi. le théorème d'Al-Kashi (ou loi des cosinus) est un théorème établissant une relation entre deux longueurs de côtés et la mesure d'un angle (ou la mesure de deux angles et la longueur d'un côté) dans un triangle quelconque.
Ici, "[AB]" représente la longueur qu'on cherche (celle de la bordure), "[BC]" représente le rayon du cercle interne et "[AC]" celui du cercle externe. Grâce à ça, nous pouvons rigoureusement tracer la bordure.
Cet algorithme ne fonctionne pas pour les premières valeurs de "X", incluses dans la bordure. En toute logique, comme elles sont incluses dans la bordures, nous allons juste entièrement les remplir de bordure. L'algorithme fonctionne aussi en prenant en compte les modifications dû au traçage de l'ellipse.

Délimiter le cercle par ses angles
Dessiner des arcs de cercles
Travail en cours...
